题目内容
9.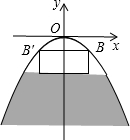 某河上由抛物线形拱桥,当水面距拱顶5m时,水面宽8m,一木船宽4m,高2m,载货后,木船露出水面的部分为$\frac{3}{4}$m,问:水面涨到与抛物线拱顶相距多少米时,木船开始不能通航?
某河上由抛物线形拱桥,当水面距拱顶5m时,水面宽8m,一木船宽4m,高2m,载货后,木船露出水面的部分为$\frac{3}{4}$m,问:水面涨到与抛物线拱顶相距多少米时,木船开始不能通航?
分析 根据题意可以求得抛物线的解析式,然后将x=2代入可以求得相应的y值,然后取此时y的绝对值与$\frac{3}{4}$相加即可解答本题.
解答 解:设抛物线的解析式为y=ax2,
∵当水面距拱顶5m时,水面宽8m,
∴抛物线过点(4,-5),
∴-5=a×42,得a=-$\frac{5}{16}$,
∴该抛物线的解析式为y=$-\frac{5}{16}{x}^{2}$,
将x=2代入y=$-\frac{5}{16}{x}^{2}$,得y=$-\frac{5}{4}$m,
$\frac{5}{4}+\frac{3}{4}$=2,
即水面涨到与抛物线拱顶相距2m时,木船开始不能通航.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
20.一个多边形中,除一个内角外,其余各内角和是120°,则这个角的度数是( )
| A. | 60° | B. | 80° | C. | 100° | D. | 120° |
17. 如图所示,根据有理数a,b,c在数轴上的位置,比较a,b,c的大小关系是( )
如图所示,根据有理数a,b,c在数轴上的位置,比较a,b,c的大小关系是( )
 如图所示,根据有理数a,b,c在数轴上的位置,比较a,b,c的大小关系是( )
如图所示,根据有理数a,b,c在数轴上的位置,比较a,b,c的大小关系是( )| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
1.计算$\frac{2m}{{m}^{2}-9}$+$\frac{1}{3-m}$的结果是( )
| A. | $\frac{1}{m-3}$ | B. | $\frac{1}{m+3}$ | C. | $\frac{3}{m-3}$ | D. | $\frac{6}{3-m}$ |
18.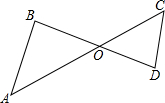 如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )
如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )
 如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )
如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )| A. | $\frac{OB}{OC}$=$\frac{OA}{OD}$ | B. | $\frac{OA}{OB}$=$\frac{OD}{OC}$ | C. | $\frac{OA}{OD}$=$\frac{AB}{CD}$ | D. | $\frac{OC}{OB}$=$\frac{OD}{OA}$ |