题目内容
14.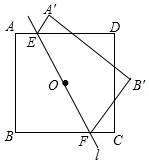 如图,正方形ABCD的边长为2,点O是正方形的中心,过点O作一条直线l分别交正方形AD,BC两边于点E,F.直线l将正方形分成两部分,将其中一部分沿这条直线翻折到另一部分上,若AE=2-$\sqrt{2}$,则两个部分图形中不重叠部分的面积为14-8$\sqrt{2}$.
如图,正方形ABCD的边长为2,点O是正方形的中心,过点O作一条直线l分别交正方形AD,BC两边于点E,F.直线l将正方形分成两部分,将其中一部分沿这条直线翻折到另一部分上,若AE=2-$\sqrt{2}$,则两个部分图形中不重叠部分的面积为14-8$\sqrt{2}$.
分析 连接OB,OB′,推出四边形BFB′O是菱形,根据菱形的性质得到OB∥B′F,推出△CFM是等腰直角三角形,△B′MN是等腰直角三角形,△A′EP与△PDN是等腰直角三角形,根据勾股定理和三角形的面积公式即可得到结论.
解答 解:连接OB,OB′,
由折叠的性质得,OB=OB′,BF=B′F,
∵四边形ABCD是正方形,点O是正方形的中心,
∴OB=$\frac{1}{2}$BD=$\sqrt{2}$,
∵一条直线l过O点,
∴CF=AE=2-$\sqrt{2}$,
∴BF=$\sqrt{2}$,
∴BO=BF=OB′=B′F,
∴四边形BFB′O是菱形,
∴OB∥B′F,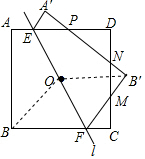
∵∠OBC=45°,
∴∠CFB′=45°,
∴△CFM是等腰直角三角形,
∴∠NMB′=∠FMC=45°,
∴△B′MN是等腰直角三角形,
同理△A′EP与△PDN是等腰直角三角形,
∴AE=A′P=CF=CM=2-$\sqrt{2}$,
∴PE=FM=2$\sqrt{2}$-2,
∴PD=DN=2-(2$\sqrt{2}$-2)-(2-$\sqrt{2}$)=2-$\sqrt{2}$,
∴PN=2$\sqrt{2}$-2,
∴NB′=MB′=2-$\sqrt{2}$,
∴两个部分图形中不重叠部分为四个全等的等腰直角三角形+梯形ABFE=4×$\frac{1}{2}$×(2-$\sqrt{2}$)2+$\frac{1}{2}$×(2-$\sqrt{2}$+2-2+$\sqrt{2}$)×2=14-8$\sqrt{2}$,
故答案为:14-8$\sqrt{2}$.
点评 本题考查了正方形的性质,翻折变换-折叠问题,菱形的判定和性质,等腰直角三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
4.一个不透明的袋子中装有仅颜色不同的2个红球和2个白球,两个人依次从袋子中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
5.下列计算正确的是( )
| A. | (3xy2)3=9x3y6 | B. | B、(x+y)2=x2+y2 | ||
| C. | x6÷x2=x3 | D. | 2x2y-$\frac{1}{2}$yx2=$\frac{3}{2}$x2y |
9. 如图所示的正六棱柱的左视图是( )
如图所示的正六棱柱的左视图是( )
 如图所示的正六棱柱的左视图是( )
如图所示的正六棱柱的左视图是( )| A. |  | B. |  | C. |  | D. |  |
6.计算(-3)-9的结果等于( )
| A. | 6 | B. | -12 | C. | 12 | D. | -6 |
4.下列汽车标志中即是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
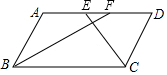 如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=3,EF=1,则BC长为( )
如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=3,EF=1,则BC长为( )