题目内容
 如图,已知点B在线段CF上,AB∥CD,AD∥BC,则S△AEF与S△BCE的大小关系
如图,已知点B在线段CF上,AB∥CD,AD∥BC,则S△AEF与S△BCE的大小关系考点:平行线之间的距离,三角形的面积
专题:
分析:连接BD,由BC∥AD.可得点F与点B到AD的距离相等,所以S△AFD=S△ABD,进而得到:S△AFD-S△AED=S△ABD-S△AED,即S△AEF=S△BED,由AB∥CD,可得点D与点C到AB的距离相等,所以S△BCE=S△BED,由等量代换可得S△AEF=S△BCE.
解答:解:连接BD,
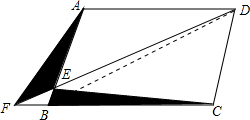
∵BC∥AD,
∴点F与点B到AD的距离相等,
∴S△AFD=S△ABD,
∴S△AFD-S△AED=S△ABD-S△AED,
即S△AEF=S△BED,
∵AB∥CD,
∴点D与点C到AB的距离相等,
∴S△BCE=S△BED,
∴S△AEF=S△BCE.
故答案为:相等.

∵BC∥AD,
∴点F与点B到AD的距离相等,
∴S△AFD=S△ABD,
∴S△AFD-S△AED=S△ABD-S△AED,
即S△AEF=S△BED,
∵AB∥CD,
∴点D与点C到AB的距离相等,
∴S△BCE=S△BED,
∴S△AEF=S△BCE.
故答案为:相等.
点评:此题考查了平行线间的距离及三角形的面积,熟记平行线间的距离相等是解题的关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 如图,正方形ABCD的边长为4cm,则它的外接圆的半径长为( )
如图,正方形ABCD的边长为4cm,则它的外接圆的半径长为( )A、
| ||
B、4
| ||
C、3
| ||
D、2
|
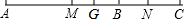 如图,G是AC的中点,M是AB的中点,N是BC的中点,那么下列四个等式中,不成立的是( )
如图,G是AC的中点,M是AB的中点,N是BC的中点,那么下列四个等式中,不成立的是( )| A、MN=GC | ||
B、MG=
| ||
C、GN=
| ||
D、MN=
|
 如图,已知AB∥CD∥EF,那么下列结论正确的是( )
如图,已知AB∥CD∥EF,那么下列结论正确的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下面几何体的截面图可能是圆的是( )
| A、正方体 | B、棱柱 |
| C、圆锥 | D、三棱锥 |
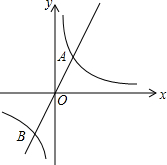 阅读理解并填空:
阅读理解并填空: 如图,△ABC绕点
如图,△ABC绕点