题目内容
国庆节期间,某超市进一批某品牌童装,下面是小阳,小佳,小欣三位营业员之间的谈话:
小阳:这批童装质量款式很好,进价才60元/件.
小佳:听经理说,该童装定价为80元/件时,每天可卖出200件.
小欣:这批童装很好卖,公司经市场调查,在定价为80元/件的基础上,每涨价1元,则每天少卖出2件.
根据她们的对话,请完成下列问题:
(1)若设该童装每件定价x元.则每件的利润是 元,(用含x的代数式表示).
(2)由于该品牌童装比较抢手,该超市决定涨价,若要每天获利5400元时,同时考虑优惠顾客,则定价应为多少元?
(3)若要使每天获利最大,则定价为多少元?最大利润是多少元?
小阳:这批童装质量款式很好,进价才60元/件.
小佳:听经理说,该童装定价为80元/件时,每天可卖出200件.
小欣:这批童装很好卖,公司经市场调查,在定价为80元/件的基础上,每涨价1元,则每天少卖出2件.
根据她们的对话,请完成下列问题:
(1)若设该童装每件定价x元.则每件的利润是
(2)由于该品牌童装比较抢手,该超市决定涨价,若要每天获利5400元时,同时考虑优惠顾客,则定价应为多少元?
(3)若要使每天获利最大,则定价为多少元?最大利润是多少元?
考点:二次函数的应用
专题:
分析:(1)利用定价-进价=每件的利润得出即可;
(2)利用销量乘以每件利润=总利润5400,进而得出即可;
(3)利用销量乘以每件利润=总利润W,再利用配方法求出函数最值.
(2)利用销量乘以每件利润=总利润5400,进而得出即可;
(3)利用销量乘以每件利润=总利润W,再利用配方法求出函数最值.
解答:解:(1)设该童装每件定价x元.则每件的利润是(x-60)元;
故答案为:(x-60);
(2)根据题意可得:(x-60)[200-2(x-80)]=5400,
解得:x1=90,x2=150(不合题意舍去),
答:定价应为90元;
(3)设总利润为:W=(x-60)[200-2(x-80)]=-2x2+480x-21600=-2(x-120)2+7200,
答:要使每天获利最大,则定价为120元,最大利润是7200元.
故答案为:(x-60);
(2)根据题意可得:(x-60)[200-2(x-80)]=5400,
解得:x1=90,x2=150(不合题意舍去),
答:定价应为90元;
(3)设总利润为:W=(x-60)[200-2(x-80)]=-2x2+480x-21600=-2(x-120)2+7200,
答:要使每天获利最大,则定价为120元,最大利润是7200元.
点评:此题主要考查了二次函数的应用以及配方法求二次函数最值,得出W与x的函数关系式是解题关键.

练习册系列答案
相关题目
有一位工人师傅将底面直径是10cm,高为80cm的“瘦长”形圆柱,锻造成底面直径为40cm的“矮胖”形圆柱,则“矮胖”形圆柱的高是( )
| A、4cm | B、5cm |
| C、6cm | D、7cm |
 大小正方形如图,小正方形边长为acm,大正方形边长为bcm,阴影面积是
大小正方形如图,小正方形边长为acm,大正方形边长为bcm,阴影面积是 如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合. 数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于
数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于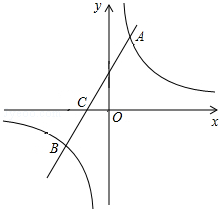 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= 如图,已知点B在线段CF上,AB∥CD,AD∥BC,则S△AEF与S△BCE的大小关系
如图,已知点B在线段CF上,AB∥CD,AD∥BC,则S△AEF与S△BCE的大小关系