题目内容
3.当“双11”购物狂欢结束后,快递小哥们的“狂欢”接踵而至.快递员不仅送件(把货物送到客户手中),也要揽件(帮客户寄出货物).南坪某快递公司针对每年“双11”期间巨大的订单物流量,制定了如表给出的送件阶梯提成激励方案,揽件提成一律按2元/件计算.| 送件数量x(件) | 提成(元/件) |
| 不超过100件的部分 | 1 |
| 超过100件不超过200件的部分 | 1.5 |
| 超过200件的部分 | 2 |
(2)去年“双11”期间,该公司安排20个快递员刚好合适.今年同期该快递公司每天送件数量大幅增加,于是加派人手,快递员人数增加了m%,同时每个快递员平均每天送件数量比(1)中所求的提成最大时的送件数量增加m%,揽件数量为(1)中相应揽件数量的一半.已知今年快递员人数多于28人,且今年“双11”期间该片区所有快递员每天获得的总提成比去年所有快递员每天获得的最大总提成多5000元.求m的值.
分析 (1)设每个快递员每天提成为y元,根据提成=送件提成+揽件提成即可得出y关于x的一次函数解析式,根据一次函数的性质即可解决最值问题;
(2)由今年快递员人数多于28人即可得出关于m的一元一次不等式,解之可得出m的取值范围,由此即可得出今年每个快递员送件件数大于210件,根据提成=送件提成+揽件提成求出今年每个快递员的提成,再根据今年“双11”期间该片区所有快递员每天获得的总提成比去年所有快递员每天获得的最大总提成多5000元即可得出关于m的一元二次方程,解之即可得出结论.
解答 解:(1)设每个快递员每天提成为y元,
根据题意得:y=2(200-x)+100×1+1.5(x-100)=-0.5x+350(150≤x≤200),
∵k=-0.5,
∴y随着x的增大而减小,
∴当x=150时,y取最大值,最大值为275.
(2)∵今年快递员人数多于28人,
∴20(1+m%)>28,
解得:m>40,
∴今年每个快递员每天送件150(1+m%)>210,
∴今年每个快递员每天提成为100×1+(200-100)×1.5+[150(1+m%)-200]×2+$\frac{50}{2}$×2=3m+200.
根据题意得:20(1+m%)(3m+200)=20×275+5000,
整理得:3m2+500m-32500=0,
解得:m=50或m=-$\frac{650}{3}$(舍去).
答:m的值为50.
点评 本题考查了一次函数的应用、一元二次方程的应用以及解一元一次不等式,解题的关键是:(1)根据数量关系提成=送件提成+揽件提成列出y关于x的一次函数关系式;(2)根据今年和去年总提成之间的关系列出关于m的一元二次方程.

练习册系列答案
相关题目
11.a,b为有理数,下列说法正确的是( )
| A. | |a+b|的值一定是正数 | B. | a2+1的值一定是正数 | ||
| C. | 当a<b时,a2<b2 | D. | 当a>b时,|a|>|b| |
18.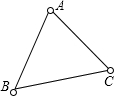 如图,兔子的三个洞口A、B、C构成△ABC,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在( )
如图,兔子的三个洞口A、B、C构成△ABC,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在( )
 如图,兔子的三个洞口A、B、C构成△ABC,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在( )
如图,兔子的三个洞口A、B、C构成△ABC,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在( )| A. | 三条边的垂直平分线的交点 | B. | 三个角的角平分线的交点 | ||
| C. | 三角形三条高的交点 | D. | 三角形三条中线的交点 |
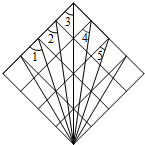 如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为225°.
如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为225°. 如图,△ABC是一块锐角三角形材料,边BC=30cm,高AD=20cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB,AC上,要使矩形EGHF的面积最大,EF的长应为15cm.
如图,△ABC是一块锐角三角形材料,边BC=30cm,高AD=20cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB,AC上,要使矩形EGHF的面积最大,EF的长应为15cm.