题目内容
11.a,b为有理数,下列说法正确的是( )| A. | |a+b|的值一定是正数 | B. | a2+1的值一定是正数 | ||
| C. | 当a<b时,a2<b2 | D. | 当a>b时,|a|>|b| |
分析 根据任何数的绝对值以及偶次方都是非负数即可对A和B判断,利用a和b的特殊值即可对C和D进行判断.
解答 解:A、当a+b=0时,|a+b|=0,不是正数,故选项错误;
B、a2≥0,则a2+1>0,则a2+1一定是正数,选项正确;
C、当x=-2,b=1时,a<b,而a2>b2,故选项错误;
D、当a=1,b=-2时,a>b,而|a|<|b|,选项错误.
故选B.
点评 本题考查了非负数的性质,以及有理数大小的比较,理解绝对值以及平方的性质是关键.

练习册系列答案
相关题目
3.当“双11”购物狂欢结束后,快递小哥们的“狂欢”接踵而至.快递员不仅送件(把货物送到客户手中),也要揽件(帮客户寄出货物).南坪某快递公司针对每年“双11”期间巨大的订单物流量,制定了如表给出的送件阶梯提成激励方案,揽件提成一律按2元/件计算.
(1)已知去年该公司每个快递员在“双11”期间平均每天送件和揽件共计200件,当送件数量x件满足150≤x≤200时,求每个快递员每天提成最大时送件数量x的值;(用函数知识说明)
(2)去年“双11”期间,该公司安排20个快递员刚好合适.今年同期该快递公司每天送件数量大幅增加,于是加派人手,快递员人数增加了m%,同时每个快递员平均每天送件数量比(1)中所求的提成最大时的送件数量增加m%,揽件数量为(1)中相应揽件数量的一半.已知今年快递员人数多于28人,且今年“双11”期间该片区所有快递员每天获得的总提成比去年所有快递员每天获得的最大总提成多5000元.求m的值.
| 送件数量x(件) | 提成(元/件) |
| 不超过100件的部分 | 1 |
| 超过100件不超过200件的部分 | 1.5 |
| 超过200件的部分 | 2 |
(2)去年“双11”期间,该公司安排20个快递员刚好合适.今年同期该快递公司每天送件数量大幅增加,于是加派人手,快递员人数增加了m%,同时每个快递员平均每天送件数量比(1)中所求的提成最大时的送件数量增加m%,揽件数量为(1)中相应揽件数量的一半.已知今年快递员人数多于28人,且今年“双11”期间该片区所有快递员每天获得的总提成比去年所有快递员每天获得的最大总提成多5000元.求m的值.
20.下列方程中是一元一次方程的是( )
| A. | 2x+y=3 | B. | 3x-1=0 | C. | $\frac{1}{x-2}=4$ | D. | 4x-1 |
 如图,在长方形ABCD中,AB=6cm,BC=8cm.动点P从点A出发,以3cm/s的速度沿逆时针方向匀速运动,当点P运动到点A时,运动停止.设点P运动的时间为t(s).
如图,在长方形ABCD中,AB=6cm,BC=8cm.动点P从点A出发,以3cm/s的速度沿逆时针方向匀速运动,当点P运动到点A时,运动停止.设点P运动的时间为t(s).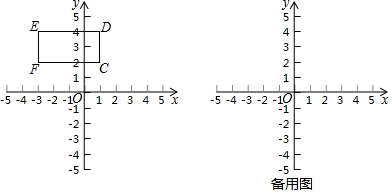
 如图l1和l2是相交于点O的两条公路,A、B是两个加油站,现准备在∠AOB的内部建一个油库,要求油库的位置点P既到A,B两个加油站的距离相等,又到两条公路l1,l2的距离相等,试用尺规作图作出点P的位置.(不写作法保留作图痕迹)
如图l1和l2是相交于点O的两条公路,A、B是两个加油站,现准备在∠AOB的内部建一个油库,要求油库的位置点P既到A,B两个加油站的距离相等,又到两条公路l1,l2的距离相等,试用尺规作图作出点P的位置.(不写作法保留作图痕迹)