题目内容
9.a、b、c是△ABC的三边,请判断4a2b2-(a2+b2-c2)2的正负.分析 原式利用平方差公式分解,再利用完全平方公式变形,继续利用平方差公式分解,利用两边之和大于第三边,两边之差小于第三边,即可确定出正负.
解答 解:4a2b2-(a2+b2-c2)2
=-(a2+b2-c2+2ab)(a2+b2-c2-2ab)
=-[(a+b)2-c2][(a-b)2-c2]
=-(a+b+c)(a+b-c)(a-b-c)(a-b+c),
∵a,b,c是三角形ABC三边,-
∴a+b+c>0,a+b-c>0,a-b-c<0,a-b+c>0,
∴-(a+b+c)(a+b-c)(a-b-c)(a-b+C)>0,
即4a2b2-(a2+b2-c2)2的值为正.
点评 此题考查了因式分解的应用,以及三角形的三边关系,将已知式子进行适当的变形是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.第31届夏季奥林匹克运动会,又称2016年里约热内卢奥运会,于2016年8月5日至8月21日在巴西的里约热内卢举行,奥运会期间,某吉祥物店在一周的销售中,盈亏情况如表(盈余为正,单位:万元)
表中星期五的盈亏数被墨水涂污了,请你算出星期五的盈亏数,并说明星期五是盈还是亏?盈亏是多少万元?
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | 合计 |
| -25.6 | -72.7 | 200 | -4 | 128.3 | 168 | 494 |
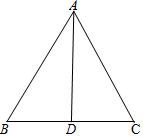 如图,在△ABC中,AB=5,BC=6,BC边上的中线AD=4.求AC的长.
如图,在△ABC中,AB=5,BC=6,BC边上的中线AD=4.求AC的长.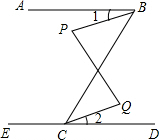 如图,已知∠ABC+∠ECB=180°,∠P=∠Q,则∠1与∠2是否相等?说说你的理由.
如图,已知∠ABC+∠ECB=180°,∠P=∠Q,则∠1与∠2是否相等?说说你的理由. 如图,AB∥CD,AD∥BC,CE=AF,则图中全等三角形有3对.
如图,AB∥CD,AD∥BC,CE=AF,则图中全等三角形有3对.