题目内容
19. 如图,AB∥CD,AD∥BC,CE=AF,则图中全等三角形有3对.
如图,AB∥CD,AD∥BC,CE=AF,则图中全等三角形有3对.
分析 根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形,进而可得AD=BC,DC=AB,然后根据平行线的性质可得∠DAF=∠BCE,再证明△ADF≌△CBE,从而可得DF=BE,然后再证明△DFC≌△BEA,△ADC≌△CBA.
解答 解:∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴AD=BC,DC=AB,
∵AD∥BC,
∴∠DAF=∠BCE,
在△ADF和△CBE中$\left\{\begin{array}{l}{AD=BC}\\{∠DAF=∠BCE}\\{AF=CE}\end{array}\right.$,
∴△ADF≌△CBE(SAS),
∴DF=BE,
∵CE=AF,
∴AE=CF,
在△DFC和△BEA中$\left\{\begin{array}{l}{DF=BE}\\{DC=AB}\\{CF=AE}\end{array}\right.$,
∴△DFC≌△BEA(SSS),
在△ADC和△CBA中$\left\{\begin{array}{l}{AD=BC}\\{AC=AC}\\{DC=AB}\end{array}\right.$,
∴△ADC≌△CBA(SSS),
全等三角形共3对,
故答案为:3,.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知AB=DC,BE=CF,只要补充∠B=∠C,或AB∥CD,就可以证明△ABE≌△DCF.
已知AB=DC,BE=CF,只要补充∠B=∠C,或AB∥CD,就可以证明△ABE≌△DCF.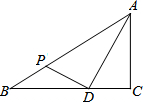 如图,△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,点P是边AB上的动点,则DP长的最小值为3cm.
如图,△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,点P是边AB上的动点,则DP长的最小值为3cm.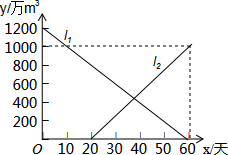 今年夏天,重庆各区持续高温日数达到历史之最,受持续高温和连日无雨的影响,重庆某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其他因素).若总蓄水量不多于900万m3为严重干旱,则该水库发生严重干旱时的天数为15≤x≤40天.
今年夏天,重庆各区持续高温日数达到历史之最,受持续高温和连日无雨的影响,重庆某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其他因素).若总蓄水量不多于900万m3为严重干旱,则该水库发生严重干旱时的天数为15≤x≤40天.