题目内容
10.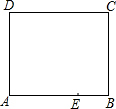 如图是一张长方形纸片ABCD,若AB=8,AD=6,E为AB上的一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5或4$\sqrt{5}$或5$\sqrt{2}$.
如图是一张长方形纸片ABCD,若AB=8,AD=6,E为AB上的一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5或4$\sqrt{5}$或5$\sqrt{2}$.
分析 分情况讨论:①当AP=AE=5时,则△AEP是等腰直角三角形,得出底边PE=$\sqrt{2}$AE=5 $\sqrt{2}$即可;
②当PE=AE=5时,求出BE,由勾股定理求出PB,再由勾股定理求出等边AP即可;
③当PA=PE时,底边AE=5;即可得出结论.
解答 解:解:如图所示: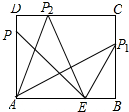
①当AP=AE=5时,
∵∠BAD=90°,
∴△AEP是等腰直角三角形,
∴底边PE=$\sqrt{2}$AE=5 $\sqrt{2}$;
②当PE=AE=5时,
∵BE=AB-AE=8-5=3,∠B=90°,
∴PB=$\sqrt{P{E}^{2}-B{E}^{2}}$=4,
∴底边AP=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4 $\sqrt{5}$;
③当PA=PE时,底边AE=5;
综上所述:等腰三角形AEP的对边长为5 $\sqrt{2}$或4 $\sqrt{5}$或5;
故答案为5或4$\sqrt{5}$或5$\sqrt{2}$.
点评 本题考查了矩形的性质、等腰三角形的判定、勾股定理;熟练掌握矩形的性质和等腰三角形的判定,进行分类讨论是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.中国的光伏技术不断进步,电子元件的尺寸大幅度缩小,在锌片上某种电子元件大约只占0.000 000 7mm2,这个数用科学记数法表示为( )
| A. | 7×10-7mm2 | B. | 0.7×10-6mm2 | C. | 7×10-8mm2 | D. | 70×10-8mm2 |
18.正方形的一条对角线长为6,则正方形的面积是( )
| A. | 9 | B. | 36 | C. | 18 | D. | 3 |
5.若一个等腰直角三角形的面积为8,则这个等腰三角形的直角边长为( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 4 | D. | 8 |
19.下列运算正确的是( )
| A. | 4x+5y=9xy | B. | (-m)3•m7=m10 | C. | (x2y)5=x2y5 | D. | a12÷a8=a4 |
4.若n(n≠0)是关于x的方程x2-mx+2n=0的根,则m-n的值为( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
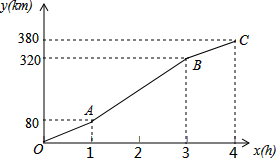 暑假期间,小刚一家乘车去离家380km的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
暑假期间,小刚一家乘车去离家380km的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示. 如图所示,正方形ABCD的边长为4,AD∥y轴,D(1,-1)
如图所示,正方形ABCD的边长为4,AD∥y轴,D(1,-1)