题目内容
13. 暑假就要来了,小明为自己制定了慢跑锻炼计划,某日小明从家出发沿解放路慢跑,已知他离家的距离s(千米)与时间t(分钟)之间的关系如图所示,请根据图象直接回答下列问题:
暑假就要来了,小明为自己制定了慢跑锻炼计划,某日小明从家出发沿解放路慢跑,已知他离家的距离s(千米)与时间t(分钟)之间的关系如图所示,请根据图象直接回答下列问题:(1)小明离开家的最远距离是多少千米,他在120分钟内共跑了多少千米;
(2)小明在这次慢跑过程中,停留所用的时间为多少分钟;
(3)小明在这段时间内慢跑的最快速度是每小时多少千米.
分析 (1)观察函数图象即可得出结论;
(2)观察函数图象二者做差即可得出结论;
(3)根据速度=路程÷时间,即可小明在这段时间内慢跑的最快速度,此题得解.
解答 解:(1)由图象知,小明离开省体育场的最远距离是4千米,他在120分钟内共跑了8千米;
(2)小明在这次慢跑过程中,停留所用的时间为:60-40=20(分钟);
(3)小明在这段时间内慢跑的最快速度是4÷$\frac{120-90}{60}$=8(千米/小时).
点评 本题考查了一次函数的应用,函数的图象,观察函数图象找出各问所用到的数据是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知点A(3,-2)、B(1,-2),则直线AB( )
| A. | 与x轴垂直 | B. | 与x轴平行 | C. | 与y轴重合 | D. | 与x、y轴相交 |
18.正方形的一条对角线长为6,则正方形的面积是( )
| A. | 9 | B. | 36 | C. | 18 | D. | 3 |
5.若一个等腰直角三角形的面积为8,则这个等腰三角形的直角边长为( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 4 | D. | 8 |
 在?ABCD中,∠A=106°,则∠C=106°.
在?ABCD中,∠A=106°,则∠C=106°.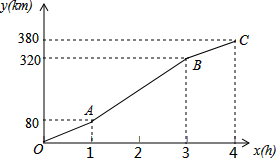 暑假期间,小刚一家乘车去离家380km的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
暑假期间,小刚一家乘车去离家380km的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示. 如图所示,正方形ABCD的边长为4,AD∥y轴,D(1,-1)
如图所示,正方形ABCD的边长为4,AD∥y轴,D(1,-1)