题目内容
20.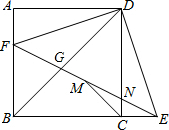 如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连结EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DN=DG;②△BFG∽△EDG∽△BDE;③CM垂直BD;④若MC=$\sqrt{2}$,则BF=2;正确的结论有( )
如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连结EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DN=DG;②△BFG∽△EDG∽△BDE;③CM垂直BD;④若MC=$\sqrt{2}$,则BF=2;正确的结论有( )| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
分析 根据正方形的性质可得AD=CD,然后利用“边角边”证明△ADF和△CDE全等,根据全等三角形对应角相等可得∠ADF=∠CDE,然后求出∠EDF=∠ADC=90°,而∠DGN=45°+∠FDG,∠DNG=45°+∠CDE,∠FDG≠∠CDE,于是∠DGN≠∠DNG,判断出①错误;根据全等三角形对应边相等可得DE=DF,然后判断出△DEF是等腰直角三角形,根据等腰直角三角形的性质可得∠DEF=45°,再根据两组角对应相等的三角形相似得到△BFG∽△EDG∽△BDE,判断出②正确;连接BM、DM,根据直角三角形斜边上的中线等于斜边的一半可得BM=DM=$\frac{1}{2}$EF,然后判断出直线CM垂直平分BD,判断出③正确;过点M作MH⊥BC于H,得到∠MCH=45°,然后求出MH,再根据三角形的中位线平行于第三边并且等于第三边的一半可得BF=2MH,判断出④正确.
解答 解:正方形ABCD中,AD=CD,
在△ADF和△CDE中,
$\left\{\begin{array}{l}{AD=AD}\\{∠A=∠DCE=90°}\\{AF=EC}\end{array}\right.$,
∴△ADF≌△CDE(SAS),
∴∠ADF=∠CDE,DE=DF,
∴∠EDF=∠FDC+∠CDE=∠FDC+∠ADF=∠ADC=90°,
∴∠DEF=45°,
∵∠DGN=45°+∠FDG,∠DNG=45°+∠CDE,∠FDG≠∠CDE,
∴∠DGN≠∠DNG,
∴DN≠DH,判断出①错误;
∵△DEF是等腰直角三角形,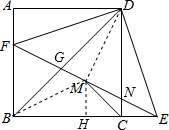
∵∠ABD=∠DEF=45°,∠BGF=∠EGD(对顶角相等),
∴△BFG∽△EDG,
∵∠DBE=∠DEF=45°,∠BDE=∠EDG,
∴△EDG∽△BDE,
∴△BFG∽△EDG∽△BDE,故②正确;
连接BM、DM.
∵△AFD≌△CED,
∴∠FDA=∠EDC,DF=DE,
∴∠FDE=∠ADC=90°,
∵M是EF的中点,
∴MD=$\frac{1}{2}$EF,
∵BM=$\frac{1}{2}$EF,
∴MD=MB,
在△DCM与△BCM中,
$\left\{\begin{array}{l}{DM=MB}\\{BC=CD}\\{CM=CM}\end{array}\right.$,
∴△DCM≌△BCM(SSS),
∴∠BCM=∠DCM,
∴CM在正方形ABCD的角平分线AC上,
∴MC垂直平分BD;故③正确;
过点M作MH⊥BC于H,则∠MCH=45°,
∵MC=$\sqrt{2}$,
∴MH=$\frac{\sqrt{2}}{2}$×$\sqrt{2}$=1,
∵M是EF的中点,BF⊥BC,MH⊥BC,
∴MH是△BEF的中位线,
∴BF=2MH=2,故④正确;
综上所述,正确的结论有②③④.
故选C.
点评 本题考查了正方形的性质,勾股定理,全等三角形的判定与性质,相似三角形的判定与性质,等腰直角三角形的判定与性质,到线段两端点距离相等的点在线段的垂直平分线,三角形的中位线平行于第三边并且等于第三边的一半,熟记各性质与定理并作辅助线是解题的关键.

| A. | 标号是奇数 | B. | 标号是3 | C. | 标号大于6 | D. | 标号小于6 |
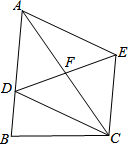 如图,在△ABC中,D为AB边上一点,F为AC的中点,连接DF并延长至E,使得EF=DF,连接AE和EC.
如图,在△ABC中,D为AB边上一点,F为AC的中点,连接DF并延长至E,使得EF=DF,连接AE和EC.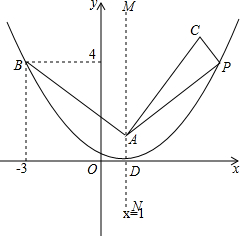 如图,在直角坐标系中,已知点A(1,1)、B(-3,4);将线段BA绕点A顺时针旋转90°得到AC;顶点为D(1,0)抛物线过点B.
如图,在直角坐标系中,已知点A(1,1)、B(-3,4);将线段BA绕点A顺时针旋转90°得到AC;顶点为D(1,0)抛物线过点B.