题目内容
 如图,⊙O是△ABC的外接圆,AD平分∠BAC,交⊙O于点D,弦DE∥BA,交AC于点F,OF与AD有怎样的位置关系,为什么?
如图,⊙O是△ABC的外接圆,AD平分∠BAC,交⊙O于点D,弦DE∥BA,交AC于点F,OF与AD有怎样的位置关系,为什么?考点:三角形的外接圆与外心,全等三角形的判定与性质
专题:
分析:设AD与CF相交于点G,连接OA,OD,根据AD平分∠BAC得出∠BAD=∠2,再由AB∥DE,得出∠BAD=∠1,故可得出∠1=∠2,即AF=DF,由SSS定理得出△AOF≌△DOF,故∠3=∠4,根据ASA定理得出△AGF≌△DGF,由此可得出结论.
解答: 解:OF垂直平分AD.
解:OF垂直平分AD.
理由:设AD与CF相交于点G,连接OA,OD,
∵OA、OD是⊙O的半径,
∴OA=OD.
∵AD平分∠BAC,
∴∠BAD=∠2.
∵AB∥DE,
∴∠BAD=∠1,
∴∠1=∠2,
∴AF=DF.
在△AOF与△DOF中,
,
∴△AOF≌△DOF(SSS),
∴∠3=∠4.
在△AGF与△DGF中,
,
∴△AGF≌△DGF(ASA),
∴AG=DG,∠AGF=∠DGF.
∵∠AGF+∠DGF=180°,
∴∠AGF=∠DGF=90°,
∴OF垂直平分AD.
 解:OF垂直平分AD.
解:OF垂直平分AD.理由:设AD与CF相交于点G,连接OA,OD,
∵OA、OD是⊙O的半径,
∴OA=OD.
∵AD平分∠BAC,
∴∠BAD=∠2.
∵AB∥DE,
∴∠BAD=∠1,
∴∠1=∠2,
∴AF=DF.
在△AOF与△DOF中,
|
∴△AOF≌△DOF(SSS),
∴∠3=∠4.
在△AGF与△DGF中,
|
∴△AGF≌△DGF(ASA),
∴AG=DG,∠AGF=∠DGF.
∵∠AGF+∠DGF=180°,
∴∠AGF=∠DGF=90°,
∴OF垂直平分AD.
点评:本题考查的是三角形的外接圆与外心,熟知角平分线的性质及全等三角形的判定与性质是解答此题的关键.

练习册系列答案
相关题目
已知三角形三边为a、b、c,其中a、b两边满足
+
=0,那么这个三角形的最大边c的取值范围是( )
| a2-12a+36 |
| b-8 |
| A、c>8 |
| B、8<c<14 |
| C、6<c<8 |
| D、2<c<14 |
 如图,CA⊥BE于点A,AD⊥BF于点D,则下列说法中正确的是( )
如图,CA⊥BE于点A,AD⊥BF于点D,则下列说法中正确的是( )| A、∠α的余角只有∠B |
| B、∠α的邻补角是∠DAC |
| C、∠α与∠ACF互补 |
| D、∠ACF是∠α的余角 |
 如图,在△ABC中,∠C=Rt∠,以顶点C为圆心,BC为半径作圆.若AC=4,tanA=
如图,在△ABC中,∠C=Rt∠,以顶点C为圆心,BC为半径作圆.若AC=4,tanA=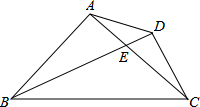 如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,若点D为△ABC外一点,且∠ADC=135°,判断BD和CD的位置关系.
如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,若点D为△ABC外一点,且∠ADC=135°,判断BD和CD的位置关系.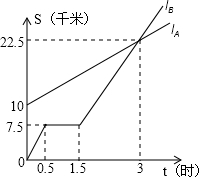 如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.