题目内容
5.联想三角形外心的概念,我们可引入如下概念:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.如图1,若PA=PB,则点P为△ABC的准外心.(1)如图2,在△ABC中,BC=6,AC=8,AB=10.D是AC上一点(非中点),且D是△ABC的一个准外心,求CD的长.
(2)如图3,在(1)的条件下,∠ABC的平分线交AC于点D.求证:$\frac{AD}{CD}$=$\frac{AB}{BC}$.
(3)在(2)的条件下,点P是△ABC的一个准外心,且点P在直线BD上,在图4中作出点P并求出BP的长.
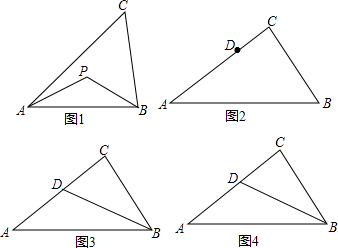
分析 (1)根据D是△ABC的一个准外心,于是分三种情况:①若DB=DA,设DA=DB=x,则x2=62+(8-x)2,即可求得CD=8-$\frac{25}{4}$=$\frac{7}{4}$,②若DA=DC,即可求得结果;③若DC=DB,由图知,P在AB上,不可能在AC上;
(2)如图3,过C作CE∥AB交BD的延长线于E,则∠E=∠ABD,由于BD平分∠ABC,得到∠ABD=∠CBD,等量代换得到∠E=∠CBD,推出CE=BC,由△ABD∽△CED,即可得到结论;
(3)如图4,分两种情况:①作线段AB的垂直平分线交AB于E,交BD于P,则点P即为所求,推出△PEB∽△BCD,得到比例式$\frac{BE}{BC}=\frac{BP}{BD}$,代入有关数据即可求得PB=$\frac{5\sqrt{5}}{2}$,②作线段BC的垂直平分线交BC于F,交BD于P′,则点P′即为所求,根据三角形的中位线的性质可得结果.
解答 解:(1)∵BC=6,AB=10,AC=8,D是△ABC的一个准外心,
①若DB=DA,设DA=DB=x,则x2=62+(8-x)2,
∴x=$\frac{25}{4}$,即DA=$\frac{25}{4}$,
∴CD=8-$\frac{25}{4}$=$\frac{7}{4}$,
②若DA=DC,则DA=DC=$\frac{1}{2}$AC=4,
③若DC=DB,由图知,P在AB上,不可能在AC上.
故DC=4或$\frac{7}{4}$;
(2)如图3,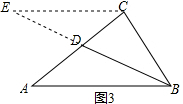 过C作CE∥AB交BD的延长线于E,
过C作CE∥AB交BD的延长线于E,
则∠E=∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠E=∠CBD,
∴CE=BC,
∵CE∥AB,
∴△ABD∽△CED,
∴$\frac{AD}{CD}=\frac{AB}{CE}$,
即$\frac{AD}{CD}=\frac{AB}{BC}$;
(3)如图4,作线段AB的垂直平分线交AB于E,交BD于P,
则点P即为所求,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠PEB=∠C=90°,
∴△PEB∽△BCD,
∴$\frac{BE}{BC}=\frac{BP}{BD}$,
由(2)知$\frac{AD}{CD}=\frac{AB}{BC}$,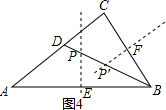
∴$\frac{AD}{CD}=\frac{10}{6}$=$\frac{5}{3}$,
∴AD=5,CD=3,
∴BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=3$\sqrt{5}$,
∵BE=$\frac{1}{2}$AB=5,
∴$\frac{5}{6}=\frac{PB}{3\sqrt{5}}$,
∴PB=$\frac{5\sqrt{5}}{2}$,
作线段BC的垂直平分线交BC于F,交BD于P′,
则点P′即为所求,
∴P′F∥CD,
∴P′B=$\frac{1}{2}$BD=$\frac{3\sqrt{5}}{2}$.
点评 本题考查了线段垂直平分线的性质,等腰三角形的性质,勾股定理,读懂题意,弄清楚准外心的定义是解题的关键.

 阅读快车系列答案
阅读快车系列答案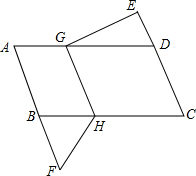 如图,已知矩形ABCD,AB=3,BC=6,E在CD的延长线上且DE=1,F在AB的延长线上且BF=2,G是AD上的一个动点,GH⊥BC于H,连接GE、FH,则当EG+GH+HF的值最小时,AG=5.
如图,已知矩形ABCD,AB=3,BC=6,E在CD的延长线上且DE=1,F在AB的延长线上且BF=2,G是AD上的一个动点,GH⊥BC于H,连接GE、FH,则当EG+GH+HF的值最小时,AG=5. 已知一次函数y=kx+b与x轴交于A点,与y轴交于B点,反比例函数y=-$\frac{k}{x}$(x>0)与直线AB只有一个交点,求S△AOB的值.
已知一次函数y=kx+b与x轴交于A点,与y轴交于B点,反比例函数y=-$\frac{k}{x}$(x>0)与直线AB只有一个交点,求S△AOB的值. 如图所示,D为等边△ABC内一点,△ABD经过旋转后到达△ACP的位置,旋转中心是哪一点,旋转角度是多少?
如图所示,D为等边△ABC内一点,△ABD经过旋转后到达△ACP的位置,旋转中心是哪一点,旋转角度是多少?