题目内容
14.等腰三角形的内角中,有一个角是另一个角的两倍,则其中三个内角的度数分别为90°、45°、45°或36°、72°、72°.分析 设出其中的一个角,建立方程求解,注意要分两种情况:当顶角是底角的两倍时和当底角是顶角的两倍时两种情况进行讨论.
解答 解:当顶角是底角的两倍时,设底角是x,则有2x+x+x=180°,
解得x=45°,
所以三角形各角分别为90°、45°、45°;
当底角是顶角的两倍时,设顶角是x,则有x十2x+2x=180°,
解得x=36°,
所以三角形各角分别为36°、72°、72°.
综上所述,三角形各角分别为90°、45°、45°或36°、72°、72°.
故答案为:90°、45°、45°或36°、72°、72°.
点评 本题考查了等腰三角形的性质及三角形内角和定理;做题时,很易漏掉一种情况,所以分类讨论的应用是正确解答本题的关键.

练习册系列答案
相关题目
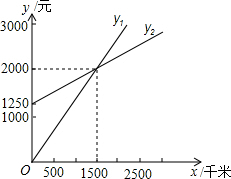 某单位准备租用一辆汽车,设汽车每月行驶x km,甲,乙两个出租车公司的月收费分别为y1元和y2元,y1,y2与x之间的函数关系图象如图,观察图象回答下列问题:
某单位准备租用一辆汽车,设汽车每月行驶x km,甲,乙两个出租车公司的月收费分别为y1元和y2元,y1,y2与x之间的函数关系图象如图,观察图象回答下列问题: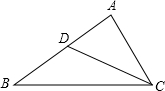 如图,在△ABC中,点D在边AB上,满足∠ACD=∠ABC,则△ADC∽△ACB,若AC=2,AD=1,则DB=3.
如图,在△ABC中,点D在边AB上,满足∠ACD=∠ABC,则△ADC∽△ACB,若AC=2,AD=1,则DB=3.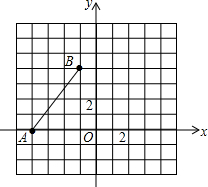 如图,已知A(-4,0),B(-1,4),将线段AB绕点O,顺时针旋转90°,得到线段A′B′.
如图,已知A(-4,0),B(-1,4),将线段AB绕点O,顺时针旋转90°,得到线段A′B′.