题目内容
13.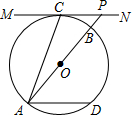 如图,已知A、C、D为⊙O上三点,过C的切线MN与弦AD平行,AD=2,AC=$\sqrt{5}$,延长AO交⊙O于B,交MN于P,则S△ACP=( )
如图,已知A、C、D为⊙O上三点,过C的切线MN与弦AD平行,AD=2,AC=$\sqrt{5}$,延长AO交⊙O于B,交MN于P,则S△ACP=( )| A. | $\frac{5}{2}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | $\frac{3}{2}\sqrt{5}$ |
分析 延长CO交AD于E,根据切线的性质得到OC⊥MN,根据平行线的性质、勾股定理求出CE,设⊙O的半径为r,根据勾股定理列出方程,解方程求出r,证明△AOE∽△POC,根据相似三角形的性质求出CP,根据三角形的面积公式计算即可.
解答 解:延长CO交AD于E,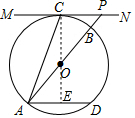
∵MN是⊙O的切线,
∴OC⊥MN,
∵MN∥AD,
∴CE⊥AD,
∴AE=DE=1,
∴CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=2,
设⊙O的半径为r,
在Rt△AOE中,r2=12+(2-r)2,
解得,r=$\frac{5}{4}$,
∴OE=CE-OC=$\frac{3}{4}$,
∵MN∥AD,
∴△AOE∽△POC,
∴$\frac{CP}{AE}$=$\frac{CO}{OE}$,即$\frac{CP}{1}$=$\frac{\frac{5}{4}}{\frac{3}{4}}$,
解得,CP=$\frac{5}{3}$,
∴S△ACP=$\frac{1}{2}$×CP×CE=$\frac{5}{3}$,
故选:B.
点评 本题考查的是切线的性质、勾股定理的应用、相似三角形的判定和性质的应用,掌握圆的切线垂直于经过切点的半径是解题的关键.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
4.方程组$\left\{\begin{array}{l}{3x-5y=2a}\\{2x+7y=a-18}\end{array}\right.$的解互为相反数,则a的值是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
5.把式子m$\sqrt{-\frac{1}{m}}$中根号外的m移到根号内,得( )
| A. | -$\sqrt{n}$ | B. | $\sqrt{-m}$ | C. | -$\sqrt{-m}$ | D. | -$\sqrt{m}$ |
2. 已知一次函数y=kx+b的图象如图所示,则关于z的不等式k(z-4)-2b>0的解集为( )
已知一次函数y=kx+b的图象如图所示,则关于z的不等式k(z-4)-2b>0的解集为( )
 已知一次函数y=kx+b的图象如图所示,则关于z的不等式k(z-4)-2b>0的解集为( )
已知一次函数y=kx+b的图象如图所示,则关于z的不等式k(z-4)-2b>0的解集为( )| A. | z>-2 | B. | z>2 | C. | z<-2 | D. | z<3 |
3.二次函数y=ax2+bx+c的图象的顶点坐标是(2,3),则a,b,c取值可以是( )
| A. | a=1,b=4,c=7 | B. | a=1,b=-4,c=1 | C. | a=2,b=8,c=5 | D. | a=-2,b=8,c=-5 |
 如图,是由一个圆柱体和一个长方体组成的几何体,其俯视图是( )
如图,是由一个圆柱体和一个长方体组成的几何体,其俯视图是( )


