题目内容
18．
如图，点A是抛物线y=a（x-3）2+k与y轴的交点，AB∥x轴交抛物线另一点于B，点C为该抛物线的顶点，若△ABC为等边三角形，则a值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | 1 |
分析 根据抛物线解析式求出对称轴为x=3，再根据抛物线的对称性求出AB的长度，然后根据CD=3$\sqrt{3}$列方程求解即可．
解答 
解：过C作CD⊥AB于D，
∵抛物线y=a（x-3）2+k的对称轴为x=3，△ABC为等边三角形，且AB∥x轴，
∴AD=3，CD=3$\sqrt{3}$，C（3，k）
∵当x=0时，y=9a+k，
∴A（0，9a+k），
∴9a+k-k=3$\sqrt{3}$，
∴a=$\frac{\sqrt{3}}{3}$．
故选C．
点评 本题考查了二次函数的性质，等边三角形的性质，熟练掌握抛物线的对称轴与两个对称点之间的关系是解题的关键．
练习册系列答案
相关题目
8．直线y=-2（x-1）+1与水平线所夹锐角的余弦是（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | -$\frac{\sqrt{5}}{5}$ |
9．签筒中有4根纸签，上面分别标有数字1，2，3，4，从中随机抽取一根，下列事件属于必然事件的是（ ）
| A． | 抽到的纸签上标有的数字小于0 | B． | 抽到的纸签上标有的数字是3 | ||
| C． | 抽到的纸签上标有的数字不小于1 | D． | 抽到的纸签上标有的数字大于4 |
6．某工厂生产一种合金薄板（其厚度忽略不计）这些薄板的形状均为正方形，边长（单位：cm）在5～50之间，每张薄板的成本价（单位：元）与它的面积（单位：cm2）成正比例，每张薄板的出厂价（单位：元）由基础价和浮动价两部分组成，（即出厂价=基础价+浮动价）其中基础价与薄板的大小无关，是固定不变的，浮动价与薄板的边长x成正比例，在营销过程中得到了表格中的数据，已知出厂一张边长为40cm的薄板，获得利润是26元．（利润=出厂价-成本价）
（1）求一张薄板的出厂价y与边长x之间满足的函数关系式；
（2）求一张薄板的利润p与边长x之间的函数关系式；
（3）若一张薄板的利润是34元，且成本最低，此时薄板的边长为多少？当薄板的边长为多少时，所获利润最大，求出这个最大值．
| 薄板的边长（cm） | 20 | 30 |
| 出厂价（元/张） | 50 | 70 |
（2）求一张薄板的利润p与边长x之间的函数关系式；
（3）若一张薄板的利润是34元，且成本最低，此时薄板的边长为多少？当薄板的边长为多少时，所获利润最大，求出这个最大值．
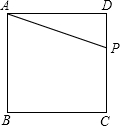如图，正方形ABCD的边长为4cm，点P从点D出发，沿边DC，CB，BA运动（点P与A重合时停止运动）．设P点运动的速度为1cm/s．
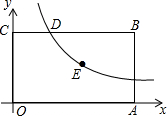如图，已知矩形OABC的一个顶点B的坐标是（4，2），反比例函数y=$\frac{k}{x}$（x＞0）的图象经过矩形的对称中点E，且与边BC交于点D，若过点D的直线y=mx+n将矩形OABC的面积分成3：5的两部分，则此直线的解析式为y=-2x+4或y=-$\frac{2}{3}$x+$\frac{8}{3}$．