题目内容
7.在⊙O中,AB为直径,AB=10,点M、N均在⊙O上,MN⊥AB,将⊙O沿MN翻折,翻折后点D与点B对应,当AD=2时,MD的长为2$\sqrt{10}$或2$\sqrt{15}$.分析 连接OM,根据垂径定理PM=PN,由折叠的性质得出DB=8或12,进而求得OP=1,由勾股定理求得PM,然后根据勾股定理即可求得MD的长.
解答  解:连接OM,
解:连接OM,
∵AB为直径,MN⊥AB,
∴PM=PN,
∵AB=10,AD=2,
∴DB=8或12,
∴PD=PB=4或6,DO=3或7,
∴OP=1,
∴PM=$\sqrt{{5}^{2}-{1}^{2}}$=2$\sqrt{6}$,
∴DM=$\sqrt{P{D}^{2}+P{M}^{2}}$=$\sqrt{{4}^{2}+(2\sqrt{6)}}$=2$\sqrt{10}$,
或DM=$\sqrt{P{D}^{2}+P{M}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{6)^{2}}}$=2$\sqrt{15}$.
故答案为2$\sqrt{10}$或2$\sqrt{15}$.
点评 本题考查了垂径定理,对称的性质,以及勾股定理的应用,作出辅助线求得PM的长是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
18. 如图,点A是抛物线y=a(x-3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点,若△ABC为等边三角形,则a值为( )
如图,点A是抛物线y=a(x-3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点,若△ABC为等边三角形,则a值为( )
 如图,点A是抛物线y=a(x-3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点,若△ABC为等边三角形,则a值为( )
如图,点A是抛物线y=a(x-3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点,若△ABC为等边三角形,则a值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 1 |
8.在-$\sqrt{3}$,-1.5,-$\sqrt{2}$,-1这四个实数中,最小的实数是( )
| A. | -$\sqrt{3}$ | B. | -1.5 | C. | $-\sqrt{2}$ | D. | -1 |
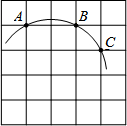 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点.
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点.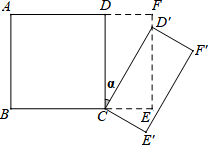 如图所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.当点D′恰好落在EF边上时,旋转角α的值为30°.
如图所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.当点D′恰好落在EF边上时,旋转角α的值为30°. 如图,AB=AC,BE与CF交于点O,且BO=CO,求证:∠B=∠C.
如图,AB=AC,BE与CF交于点O,且BO=CO,求证:∠B=∠C.