题目内容
3.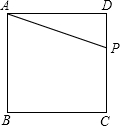 如图,正方形ABCD的边长为4cm,点P从点D出发,沿边DC,CB,BA运动(点P与A重合时停止运动).设P点运动的速度为1cm/s.
如图,正方形ABCD的边长为4cm,点P从点D出发,沿边DC,CB,BA运动(点P与A重合时停止运动).设P点运动的速度为1cm/s.①求△APD的面积y关于时间t的函数关系式;
②分别求t=4和10时,y的值;
③t为何值时,△APD面积最大,最大面积是多少?
分析 ①分三种情况分别计算△APD的面积y:
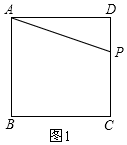
i)当P在DC上时,0≤t≤4,如图1,
ii)当P在BC上时,4<t≤8,如图2,
iii)当P在AB上时,8<t≤12,如图3,
②分别代入①中对应的y与t的关系式中,求出即可;
③分别根据三种情况的关系式的增减性讨论可得结论.
解答 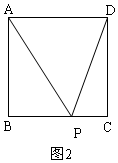
 解:①分三种情况:
解:①分三种情况:
i)当P在DC上时,0≤t≤4,如图1,
由题意得是:PD=t,
∴y=$\frac{1}{2}$AD•PD=$\frac{1}{2}$×4t=2t;
ii)当P在BC上时,4<t<8,如图2,
∴y=$\frac{1}{2}$AD•AB=$\frac{1}{2}$×4×4=8;
iii)当P在AB上时,8≤t≤12,如图3,
由题意得:DC+BC+BP=t,则AP=12-t,
∴y=$\frac{1}{2}$AP•AD=$\frac{1}{2}$×4×(12-t)=2(12-t)=-2t+24;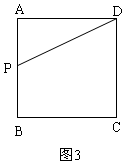
综上所述,y关于时间t的函数关系式为:y=$\left\{\begin{array}{l}{2t(0≤t≤4)}\\{8(4<t<8)}\\{-2t+24(8≤t≤12)}\end{array}\right.$;
②当t=4时,y=2t=2×4=8cm2;
当t=10时,y=-2t+24=-2×10+24=4cm2;
③当0≤t≤4时,t=4时,y有最大值为8,
当4<t<8时,y大=8,
当8≤t≤12,y=-2t+24,
∵-2<0,
∴y随t的增大而减小,
∴当x=8时,y有最大值是8,
综上所述,当4≤t≤8时,△APD面积最大,最大面积是8cm2.
点评 本题是四边形和函数的综合题,考查了正方形的性质、三角形的面积、动点运动问题、一次函数的最值问题,难度适中,正确表示不同时间段点P运动的路程是关键,注意利用数形结合的思想解决问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 316 | B. | $\frac{{\sqrt{198}}}{2}$ | C. | 50.5 | D. | 39.5 |
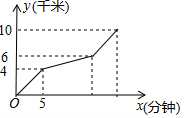 如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )
如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )| A. | 15分钟 | B. | 20分钟 | C. | 25分钟 | D. | 30分钟 |
 如图,点A是抛物线y=a(x-3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点,若△ABC为等边三角形,则a值为( )
如图,点A是抛物线y=a(x-3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点,若△ABC为等边三角形,则a值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 1 |
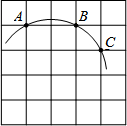 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点.
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点.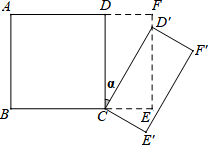 如图所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.当点D′恰好落在EF边上时,旋转角α的值为30°.
如图所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.当点D′恰好落在EF边上时,旋转角α的值为30°.