题目内容
11.函数y=x+1的图象与x轴、y轴围成三角形的面积为$\frac{1}{2}$.分析 分别求出函数与x轴,y轴交点的坐标,即可求得面积.
解答 解:令x=0,解得y=1,即函数与y轴交点坐标为(0,1),
令y=0,解得x=-1,即函数与x轴交点坐标为(-1,0),
所以,图象与x轴,y轴围成的三角形面积s=$\frac{1}{2}$×1×1=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了一次函数图象上点的坐标特征,是基础题型.

练习册系列答案
相关题目
6.下列说法不一定成立的是( )
| A. | 若a>b,则c-a<c-b | B. | 若c-a<c-b,则a>b | C. | 若a<b,则ac2<bc2 | D. | 若ac2<bc2,则a<b |
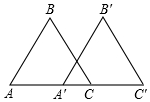 如图,△A′B′C′是由△ABC沿射线AC方向平移20cm得到,若AC=30cm,则A′C=10cm.
如图,△A′B′C′是由△ABC沿射线AC方向平移20cm得到,若AC=30cm,则A′C=10cm.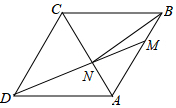 如图,在边长为6的菱形ABCD中,点M在AB边上,DM交AC于点N,连接BN
如图,在边长为6的菱形ABCD中,点M在AB边上,DM交AC于点N,连接BN