题目内容
12.阅读材料:本册数学学习中,我们认识了“完全平方公式”,即(a±b)2=a2±2ab+b2,并把形如a2±2ab+b2的式子称为完全平方式.把形如ax2+bx+c(a≠0)的二次三项式(或其一部分)配成完全平方式的过程叫配方.配方的基本形式是完全平方公式的逆写,即a2±2ab+b2=(a±b)2.例如
①选取二次项和一次项配方:x2-2x+4=(x-1)2+3;
②选取二次项和常数项配方:x2-2x+4=(x+2)2-6x,
或x2-2x+4=(x-2)2+2x;
③选取一次项和常数项配方:x2-2x+4=($\frac{1}{2}$x-2)2+$\frac{3}{4}$x2.
根据上述材料,解决下面问题:
(1)写出x2+4x+9的两种不同形式的配方;
(2)已知4x2+y2-4x+6y+10=0,求xy的值;
(3)试求当x为何值时,-x2+4x+5有最大值,最大值是多少?
分析 (1)根据材料选择①②两种方法进行配方即可;
(2)将等式的左边分解因式后利用非负数的性质求得x、y的值后即可求得代数式的值;
(3)将二次三项式进行配方后即可求得最值.
解答 解:(1)x2+4x+9=(x+2)2+5;
x2+4x+9=(x+3)2-2x;
(2)配方得:4x2-4x+1+y2+6y+9=0,
即:(2x-1)2+(y+3)2=0,
故2x-1=0,y+3=0,
解得:x=$\frac{1}{2}$,y=-3,
所以xy=($\frac{1}{2}$)-3=8;
(3)∵-x2+4x+5=-(x2-4x+4-4)+5=-(x-2)2+9,
∴当x为2时有最小值为9.
点评 本题考查了配方法的应用,解题的关键是能够根据阅读材料进行配方,难度不大.

练习册系列答案
相关题目
2.已知⊙O1和⊙O2相切,⊙O1的半径为2cm,⊙O2的半径为3cm,则O1O2的长是( )
| A. | 1cm | B. | 5cm | C. | 1cm或5cm | D. | 0.5cm或2.5cm |
3.下列函数,当x>0时,y随x的增大而增大的是( )
| A. | y=-2x | B. | y=$\frac{2}{x}$ | C. | y=2x-1 | D. | y=-x2+1 |
20.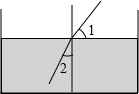 如图,当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象.图中∠1=47°,∠2=30°,则光的传播方向改变的度数为( )
如图,当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象.图中∠1=47°,∠2=30°,则光的传播方向改变的度数为( )
 如图,当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象.图中∠1=47°,∠2=30°,则光的传播方向改变的度数为( )
如图,当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象.图中∠1=47°,∠2=30°,则光的传播方向改变的度数为( )| A. | 13° | B. | 15° | C. | 17° | D. | 19° |
17. 如图,光源P在水平放置的横杆AB的正上方,AB在灯光下的影子CD也呈水平状态,AB=2m,CD=6m,点P到CD的距离是3.9m,则AB与CD之间的距离是( )
如图,光源P在水平放置的横杆AB的正上方,AB在灯光下的影子CD也呈水平状态,AB=2m,CD=6m,点P到CD的距离是3.9m,则AB与CD之间的距离是( )
 如图,光源P在水平放置的横杆AB的正上方,AB在灯光下的影子CD也呈水平状态,AB=2m,CD=6m,点P到CD的距离是3.9m,则AB与CD之间的距离是( )
如图,光源P在水平放置的横杆AB的正上方,AB在灯光下的影子CD也呈水平状态,AB=2m,CD=6m,点P到CD的距离是3.9m,则AB与CD之间的距离是( )| A. | 2.6m | B. | 2m | C. | 1.3m | D. | 1m |
4.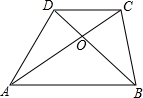 如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )
如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )
 如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )
如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.多项式36a3b2-18a2b3+12a2b2各项的公因式是( )
| A. | a2b2 | B. | 12a3b3 | C. | 6a3b3 | D. | 6a2b2 |
 如图是一副三角板拼成的图案,∠AED=135°.
如图是一副三角板拼成的图案,∠AED=135°.