题目内容
18.抛物线y=x2+bx+c经过A(-1,-1)、B(1,3)两点.求抛物线的解析式.分析 把点A(-1,-1)、B(1,3)分别代入二次函数y=x2+bx+c得到关于b与c的方程组,然后解方程组求出b、c即可.
解答 解:把点A(-1,-1)、B(1,3)分别代入y=x2+bx+c得,
$\left\{\begin{array}{l}{1-b+c=-1}\\{1+b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=0}\end{array}\right.$,
∴抛物线解析式为y=x2+2x.
点评 本题考查了利用待定系数法求二次函数的解析式:设二次函数的解析式为y=ax2+bx+c(a≠0),然后把图象上三个点的坐标分别代入得到关于a、b、c的方程组,解方程组求出a、b、c的值,从而确定二次函数的解析式.

练习册系列答案
相关题目
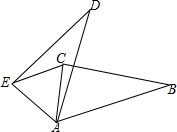 在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得DE∥AB,则∠DAB等于30°.
在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得DE∥AB,则∠DAB等于30°.