题目内容
18.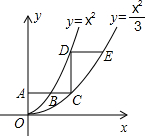 如图,平行于x轴的直线AC分别交抛物线${y_1}={x^2}$(x≥0)与${y_2}=\frac{x^2}{3}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E.若已知点A的纵坐标为1,则CD的长度为2,$\frac{DE}{AB}$=3-$\sqrt{3}$.
如图,平行于x轴的直线AC分别交抛物线${y_1}={x^2}$(x≥0)与${y_2}=\frac{x^2}{3}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E.若已知点A的纵坐标为1,则CD的长度为2,$\frac{DE}{AB}$=3-$\sqrt{3}$.
分析 根据待定系数法求出点A、B、C、D、E坐标即可解决问题.
解答 解:由题意,点A(0,1),点B(1,1),点C($\sqrt{3}$,1),点D($\sqrt{3}$,3),点E(3,3).
∴CD=3-1=2,DE=3-$\sqrt{3}$,AB=1,
∴$\frac{DE}{AB}$=3-$\sqrt{3}$.
故答案分别为2,3-$\sqrt{3}$.
点评 本题考查一次函数图象上的点的特征,掌握待定系数法是解决问题的关键,知道平行于x轴的两点纵坐标相同,平行于y轴的两点的横坐标相同,属于中考常考题型.

练习册系列答案
相关题目
6. (1)画出函数y=-$\frac{6}{x}$(x<0)的图象:
(1)画出函数y=-$\frac{6}{x}$(x<0)的图象:
列表:
描点并连线.
(2)从图象可以看出,曲线从左向右依次升高,当x由小变大时,y=-$\frac{6}{x}$(x<0)随之变大.
 (1)画出函数y=-$\frac{6}{x}$(x<0)的图象:
(1)画出函数y=-$\frac{6}{x}$(x<0)的图象:列表:
| x | … | -6 | -5 | -4 | -3 | -2 | -1 | … |
| y | … | … |
(2)从图象可以看出,曲线从左向右依次升高,当x由小变大时,y=-$\frac{6}{x}$(x<0)随之变大.
3.若直线y=kx+b(k<0,b>0)的大致图象为( )
| A. |  | B. |  | C. |  | D. |  |
8.下图是上海今年春节七天最高气温(℃)的统计结果:
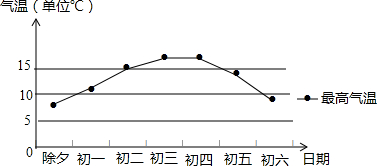
这七天最高气温的众数和中位数是( )

这七天最高气温的众数和中位数是( )
| A. | 15,17 | B. | 14,17 | C. | 17,14 | D. | 17,15 |
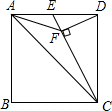 如图,在正方形ABCD中,E是AD的中点,DF⊥EC于点F,连结AF,则下列四个结论:
如图,在正方形ABCD中,E是AD的中点,DF⊥EC于点F,连结AF,则下列四个结论: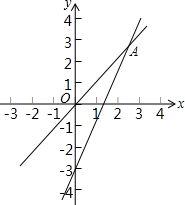 已知一个正比例函数与一个一次函数的图象交于点A(3,4),且0A=0B
已知一个正比例函数与一个一次函数的图象交于点A(3,4),且0A=0B
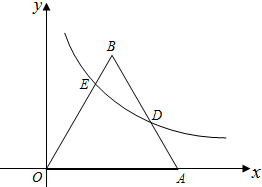 如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过AB边的中点D,交OB边于点E.
如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过AB边的中点D,交OB边于点E.