如图.在四边形ABCD中.E.F分别是AB.AD的中点.若EF=2.BC=5.CD=3.求△DBC的面积．题目和参考答案——青夏教育精英家教网——

题目内容

18．

如图，在四边形ABCD中，E，F分别是AB，AD的中点，若EF=2，BC=5，CD=3，求△DBC的面积．

分析根据三角形中位线定理，可得BD的长，根据勾股定理逆定理，可得△BCD是直角三角形，根据三角形的面积公式，可得答案．

解答解：在△ABD中，由三角形中位线定理，得
BD=2EF=4．
由BD²+CD²=4²+3²=25，BC²=5²=25，得
BD²+CD²=BC²，
∠BDC=90°．
由三角形的面积公式，得
S_△DBC=$\frac{1}{2}$BD•CD=$\frac{1}{2}$×4×3=6．

点评本题考查了三角形的中位线，利用了三角形的中位线定理，利用勾股定理的逆定理得出直角三角形是解题关键．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

某校对200名学生进行“最爱看电视节目”调查，得到如图扇形统计图，其中最爱看文艺类节目的学生有80人．

9．已知：△ABC中，∠C＞∠B，AE平分∠BAC．
（1）如图①AD⊥BC于D，若∠C=70°，∠B=30°，求出∠DAE的度数；
（2）若△ABC中，∠B=α，∠C=β（α＜β），探索∠DAE与α、β间的等量关系，不必说明理由；
（3）如图②所示，在△ABC中AD⊥BC，AE平分∠BAC，F是AE上的任意一点，过F作FG⊥BC于G，且∠B=
30°，∠C=80°，请你运用（2）中结论求出∠EFG的度数；
（4）在（3）的条件下，若F点在AE的延长线上（如图③），其他条件不变，则∠EFG的度数大小发生改变吗？说明理由．

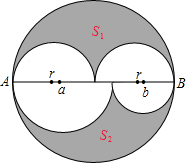如图，大圆的半径为r，直径AB上方两个半圆的直径均为r，下方两个半圆的直径分别为a，b．
（1）求直径AB上方阴影部分的面积S₁；
（2）用含a，b的代数式表示直径AB下方阴影部分的面积S₂=$\frac{1}{4}πab$；
（3）设a=r+c，b=r-c（c＞0），那么（　　）
（A）S₂=S₁；（B）S₂＞S₁；（C）S₂＜S₁；（D）S₂与S₁的大小关系不确定；
（4）请对你在第（3）小题中所作的判断说明理由．

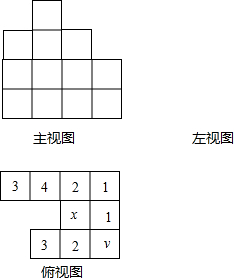如图是几个小立方体搭成的几何体的俯视图，小正方形中的数字表示该位置上的小立方体的个数．
（1）确定x、y的值；
（2）完成这个几何体的左视图．

已知，直线AB，CD被直线EF所截，AB∥CD，NG是∠END的角平分线，交AB于点O，如果∠1=50°，则∠ENC=80°．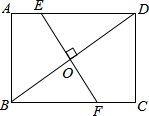

如图，在矩形ABCD中，AB=3cm，AD=4cm，过对角线BD的中点O作BD的垂线EF，分别交AD，BC于点E，F，求AE的长．

在某个奔跑活动中，有一个边长为10m正方形路线图，两名选手甲，乙同时从起点A沿着箭头方向绕路线图奔跑，两人第一次相遇在BC的中点O处，当两名选手第一次在点A处相遇时，选手乙已经跑了200m．

8．解方程：x²+3x=1．