题目内容
3. 实数a,b,c在数轴上对应点的位置如图所示,则$\root{3}{{a}^{3}}$+|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|=a-2b.
实数a,b,c在数轴上对应点的位置如图所示,则$\root{3}{{a}^{3}}$+|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|=a-2b.
分析 先根据各点在数轴上的位置判断出其符号及绝对值的大小,进而可得出结论.
解答 解:∵由图可知,a<b<0<c,
∴a+b<0,c-a>0,b-c<0
∴原式=a-(a+b)-(c-a)+(c-b)
=a-a-b-c+a+c-b
=a-2b.
故答案为:a-2b.
点评 本题考查的是实数与数轴,熟知数轴上各点与实数是一一对应关系是解答此题的关键.

练习册系列答案
相关题目
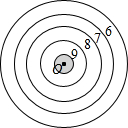 如图所示,小明在劳动课上做了一个靶子,靶心圆的半径为2cm,击中为10环(阴影部分),向外依次是9,8,7,6环,10,9,8,7,6圆环间距离都是3cm.
如图所示,小明在劳动课上做了一个靶子,靶心圆的半径为2cm,击中为10环(阴影部分),向外依次是9,8,7,6环,10,9,8,7,6圆环间距离都是3cm. 如图,AD、BC是⊙O的两条互相垂直的直径,点P从O点出发,沿0CDO的路线匀速运动,设点P运动的时间为x(单位:秒),∠APB=y(单位:度),那么表示y与x之间关系的图象是( )
如图,AD、BC是⊙O的两条互相垂直的直径,点P从O点出发,沿0CDO的路线匀速运动,设点P运动的时间为x(单位:秒),∠APB=y(单位:度),那么表示y与x之间关系的图象是( )


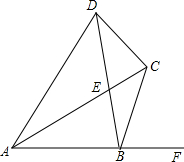 已知:AB=2,AC平分∠DAB,∠DAB+∠DCB=180°,∠DCB=120°,当∠ABD=∠CBF时,则AC=$\sqrt{3}$+1.
已知:AB=2,AC平分∠DAB,∠DAB+∠DCB=180°,∠DCB=120°,当∠ABD=∠CBF时,则AC=$\sqrt{3}$+1.