题目内容
5.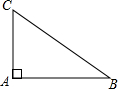 如图,在△ABC中,∠A=90°,若AB=8,AC=6,则cosC的值为( )
如图,在△ABC中,∠A=90°,若AB=8,AC=6,则cosC的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 根据勾股定理求出BC,根据余弦的定义计算即可.
解答 解:∵∠A=90°,AB=8,AC=6,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=10,
∴cosC=$\frac{AC}{BC}$=$\frac{6}{10}$=$\frac{3}{5}$,
故选:A.
点评 本题考查的是锐角三角函数的定义,掌握锐角A的邻对边a与斜边c的比叫做∠A的余弦是解题的关键.

练习册系列答案
相关题目
15.下列方程中两个实数根的和等于2的方程是( )
| A. | 2x2-4x+3=0 | B. | 2x2-2x-3=0 | C. | 2y2+4y-3=0 | D. | 2t2-4t-3=0 |
16.单项式-$\frac{2{x}^{3}{y}^{2}z}{3}$的系数是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
13.二次函数y=-x2-2x+3的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
20.不等式组$\left\{\begin{array}{l}{x+2>0}\\{2x-1≤0}\end{array}\right.$的所有整数解是( )
| A. | -1、0 | B. | -2、-1 | C. | 0、1 | D. | -2、-1 |
10. 如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )
如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )
 如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )
如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )| A. | 6$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 9 | D. | 4.5 |