题目内容
1. 如图,AB,CD是两根钉在木板上的平行木条,将一根橡皮筋固定在A,C两点,点E是橡皮筋上的一点,拽动E点将橡皮筋拉紧后,请你探索∠A,∠AEC,∠C之间具有怎样的关系并说明理由.(提示:先画出示意图,再说明理由).
如图,AB,CD是两根钉在木板上的平行木条,将一根橡皮筋固定在A,C两点,点E是橡皮筋上的一点,拽动E点将橡皮筋拉紧后,请你探索∠A,∠AEC,∠C之间具有怎样的关系并说明理由.(提示:先画出示意图,再说明理由).
分析 分6种情况进行讨论,分别根据平行线的性质:两直线平行,内错角相等,两直线平行,同位角相等,即可得到结论.
解答 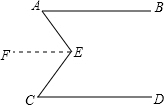 解:如图所示,∠AEC=∠A+∠C.
解:如图所示,∠AEC=∠A+∠C.
理由如下:
如图,过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠C=∠FEC;
∵AB∥EF,
∴∠A=∠AEF;
∴∠AEC=∠AEF+∠FEC=∠A+∠C.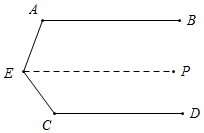
如图所示,∠AEC+∠EAB+∠ECD=360°,
理由如下:
如图,过E作EP∥AB,则AB∥PE∥CD,
∴∠BAE+∠AEF=180°,∠CEF+∠ECD=180°,
∴∠BAE+∠AEF+∠CEF+∠ECD=360°,
∴∠AEC+∠EAB+∠ECD=360°.
如图所示,∠A+∠AEC=∠C.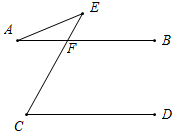
理由如下:
如图,∵AB∥CD,
∴∠C=∠BFE,
∵∠BFE是△AEF的外角,
∴∠BFE=∠A+∠E,
∴∠C=∠A+∠E.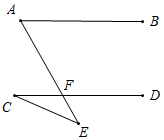
如图所示,∠C+∠E=∠A.
理由如下:
如图,∵AB∥CD,
∴∠A=∠AFC,
∵∠AFC是△CEF的外角,
∴∠AFC=∠C+∠E,
∴∠A=∠C+∠E.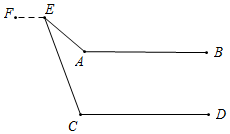
如图所示,∠A=∠C+∠AEC.
理由如下:
如图,∵过E作EF∥AB,则AB∥FE∥CD,
∴∠C=∠CEF,∠A=∠AEF,
∵∠AEF=∠CEF+∠AEC,
∴∠A=∠C+∠AEC.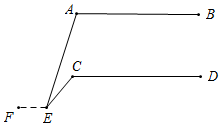
如图所示,∠C=∠A+∠AEC.
理由如下:
如图,∵过E作EF∥AB,则AB∥FE∥CD,
∴∠C=∠CEF,∠A=∠AEF,
∵∠CEF=∠AEF+∠AEC,
∴∠C=∠A+∠AEC.
点评 本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:两直线平行,内错角相等;两直线平行,同位角相等.正确作辅助线是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
9.两个锐角分别相等的两个直角三角形( )全等.
| A. | 不一定 | B. | 一定不 | C. | 一定 | D. | 以上都不对 |
 如图,在△AEC中,点D是EC上的一点,且AE=AD,AB=AC,∠1=∠2.求证:BD=EC.
如图,在△AEC中,点D是EC上的一点,且AE=AD,AB=AC,∠1=∠2.求证:BD=EC. 如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.
如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.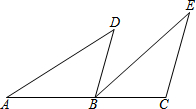 已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB.
已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB. 如图,AB是⊙O的直径,AB=2,分别以A,B为圆心,1为半径画弧与⊙O交于C,E,D,F,则阴影部分的面积是$\sqrt{3}$-$\frac{π}{3}$.
如图,AB是⊙O的直径,AB=2,分别以A,B为圆心,1为半径画弧与⊙O交于C,E,D,F,则阴影部分的面积是$\sqrt{3}$-$\frac{π}{3}$.