题目内容
10.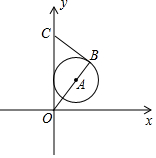 如图,已知点A的坐标为(3,4),⊙A的半径为3,延长OA交⊙A于点B,过点B作⊙A的切线,交y轴于点C,则OC长为( )
如图,已知点A的坐标为(3,4),⊙A的半径为3,延长OA交⊙A于点B,过点B作⊙A的切线,交y轴于点C,则OC长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 作AD⊥y轴于点D,可得AD=3、OD=4、∠ODA=∠OBC=90°,继而知OA=5,证△AOD∽△COB得$\frac{OA}{OC}$=$\frac{OD}{OB}$,由此可得答案.
解答 解:如图,过点A作AD⊥y轴于点D,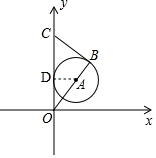
∵A的坐标为(3,4),且BC与⊙O相切,
∴AD=3、OD=4,∠ODA=∠OBC=90°,
∴$OA=\sqrt{O{D}^{2}+A{D}^{2}}$=5,
∵∠AOD=∠COB,
∴△AOD∽△COB,
∴$\frac{OA}{OC}$=$\frac{OD}{OB}$,即$\frac{5}{OC}$=$\frac{4}{5+3}$,
解得:OC=10,
故选:C.
点评 本题主要考查切线的性质及相似三角形的判定与性质,由切线的性质证得两三角形相似是解题的关键.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
1.计算正确的是( )
| A. | x2+x2=x4 | B. | x2+y2=x2y2 | C. | x2•x2=2x4 | D. | (xy2)2=x2y4 |
5.若抛物线y=-x2向右平移3个单位,再向下平移2个单位,所得的抛物线的解析式为( )
| A. | y=-(x+3)2+2 | B. | y=-(x-3)2+2 | C. | y=-(x-3)2-2 | D. | y=-(x+3)2-2 |
15.一元二次方程x2-2x=0根的判别式的值为( )
| A. | 4 | B. | 2 | C. | 0 | D. | -4 |
2.某车间有27名工人,生产某种由一个螺栓套两个螺母的产品,每人每天生产螺母16个或螺栓22个,若分配x名工人生产螺栓,其他工人生产螺母,恰好使每天生产的螺栓和螺母配套,则下面所列方程中正确的是( )
| A. | 22x=16(27-x) | B. | 16x=22(27-x) | C. | 2×16x=22(27-x) | D. | 2×22x=16(27-x) |
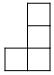
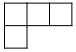
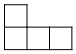
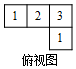 由7个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则其左视图是( )
由7个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则其左视图是( )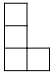




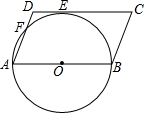 如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为π.
如图,在?ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则$\widehat{FE}$的长为π.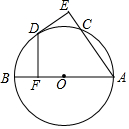 如图,AB为⊙O直径,C为⊙O上一点,点D是$\widehat{BC}$的中点,过D作⊙O的切线交AC的延长线于E,DF⊥AB于F.
如图,AB为⊙O直径,C为⊙O上一点,点D是$\widehat{BC}$的中点,过D作⊙O的切线交AC的延长线于E,DF⊥AB于F.