题目内容
9.若等式$\frac{m}{x+3}$-$\frac{n}{x-3}$=$\frac{8x}{{x}^{2}-9}$对任意的x(x≠±3)恒成立,则m=4.分析 已知等式去分母转化为整式方程,根据对任意的x(x≠±3)恒成立,确定出m的值即可.
解答 解:已知等式去分母得:m(x-3)-n(x+3)=8x,
整理得:(m-n-8)x=3(m+n),
由方程对任意的x(x≠±3)恒成立,得到$\left\{\begin{array}{l}{m-n=8}\\{m+n=0}\end{array}\right.$,
解得:m=4,n=-4.
故答案为:4.
点评 此题考查了分式的加减法,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.在$\sqrt{15}$,$\sqrt{\frac{1}{6}}$,$\sqrt{1\frac{1}{2}}$,$\sqrt{40}$,$\sqrt{0.2}$中最简二次根式的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.2015年春我国大部分地区出现严重雾霾,为了增强同学们的环保意识,某校组织了一次防治雾霾知识竞赛,两组学生成绩统计如下:
已知算得两个组的人均分数都是80分,请根据你所学过的统计知识,进一步判断这两个组这次成绩谁优谁次,并说明理由.
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人数 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
| 乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
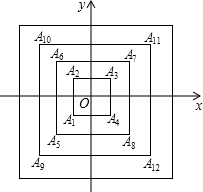 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2015的坐标是(504,504).
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2015的坐标是(504,504).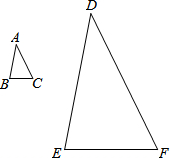 如图,△ABC∽△DEF,AB:DE=1:4,那么,需要16个△ABC才能将△DEF镶嵌满.
如图,△ABC∽△DEF,AB:DE=1:4,那么,需要16个△ABC才能将△DEF镶嵌满.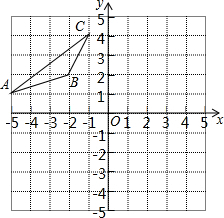 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-5,1),B(-2,2),C(-1,4),请按下列要求画图:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-5,1),B(-2,2),C(-1,4),请按下列要求画图: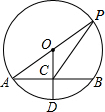 如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点P,连接PC.若AB=8,OC=3,则PC=2$\sqrt{13}$.
如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点P,连接PC.若AB=8,OC=3,则PC=2$\sqrt{13}$.