题目内容
16．解不等式组：-5＜2x+1＜6，并把解集在数轴上表示出来．分析 把原不等式组化为$\left\{\begin{array}{l}{2x+1＞-5①}\\{2x+1＜6②}\end{array}\right.$，再分别解两个不等式得到x＞-3和x＜2，然后根据大小小大中间找确定不等式组的解集，再用数轴表示解集．
解答 解：原不等式组可化为$\left\{\begin{array}{l}{2x+1＞-5①}\\{2x+1＜6②}\end{array}\right.$，
解①得x＞-3，
解②得x＜2，
所以原不等式组的解集为-3＜x＜2，
用数轴表示为：
．
点评 本题考查了解一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．
练习册系列答案
口算能手系列答案
相关题目
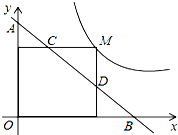如图，M为双曲线y=$\frac{2}{3x}$（x＞0）上的一点，过点M作x轴、y轴的垂线，分别交直线y=-x+m于点D、C两点．若直线y=-x+m与y轴交于点A，与x轴交于点B，则AD•BC的值为$\frac{4}{3}$．
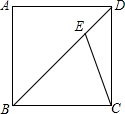如图，正方形ABCD中，E为BD上一点，∠DCE=22.5°
如图，AC平分∠BAD，∠1=∠2，哪两条线段平行？说明理由．
11．已知两直线y1=kx+k-1，y2=（k+1）x+k（k是正整数），设两条直线与x轴围成三角形的面积为Sk，则S1+S2+S3+…+S2014=（ ）
| A． | $\frac{2013}{2014}$ | B． | $\frac{2014}{2015}$ | C． | $\frac{2014}{2013}$ | D． | $\frac{1007}{2015}$ |
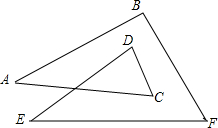在图中，猜想∠A+∠B+∠C+∠D+∠E+∠F=360°，说明你的理由．