题目内容
16. 已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.(1)求证:OE=OF.
(2)当∠DOE等于90度时,四边形BFDE为菱形.(直接填写答案即可)
分析 (1)利用全等三角形的判定方法得出△DOE≌△BOF即可得出答案;
(2)利用菱形的判定方法得出即可.
解答 (1)证明:∵四边形ABCD是平行四边形,O为对角线BD的中点,
∴BO=DO,AD∥BC
∴∠EDB=∠FBO,
在△EOD和△FOB中
$\left\{\begin{array}{l}{∠EDO=∠OBF}\\{DO=BO}\\{∠EOD=∠FOB}\end{array}\right.$,
∴△DOE≌△BOF(ASA),
∴OE=OF;
(2)解:当∠DOE=90°时,四边形BFDE为菱形.
点评 此题主要考查了全等三角形的判定与性质以及菱形的判定,得出△DOE≌△BOF是解题关键.

练习册系列答案
相关题目
6.已知关于x的一元二次方程x2+kx-k-1=0有两个相等的实数根,则k的值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
4.下列运算正确的是( )
| A. | 3a+3b=6ab | B. | a3-a=a2 | C. | (a2)3=a6 | D. | a6÷a3=a2 |
1.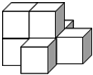 如图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是( )
如图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是( )
 如图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是( )
如图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是( )| A. | 俯视图 | B. | 主视图 | C. | 俯视图和左视图 | D. | 主视图和俯视图 |
8.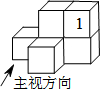 如图是由6个同样大小的正方体摆成的几何体.将标有“1”的这个正方体移走后,所得几何体( )
如图是由6个同样大小的正方体摆成的几何体.将标有“1”的这个正方体移走后,所得几何体( )
 如图是由6个同样大小的正方体摆成的几何体.将标有“1”的这个正方体移走后,所得几何体( )
如图是由6个同样大小的正方体摆成的几何体.将标有“1”的这个正方体移走后,所得几何体( )| A. | 俯视图改变,左视图改变 | B. | 主视图改变,左视图不变 | ||
| C. | 俯视图不变,主视图不变 | D. | 主视图不变,左视图改变 |
5.以下问题,不适合用全面调查的是( )
| A. | 了解全班同学每周体育锻炼的时间 | B. | 学校招聘教师,对应聘人员面试 | ||
| C. | 了解重庆庆中小学生每天的零花钱 | D. | 旅客上飞机前的安检 |