题目内容
3.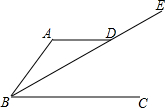 如图,AD∥BC,点E在BD的延长线上.若∠ADE=145°,则∠DBC=35°.
如图,AD∥BC,点E在BD的延长线上.若∠ADE=145°,则∠DBC=35°.
分析 先根据补角的定义求出∠ADB的度数,再由平行线的性质即可得出结论.
解答 解:∵∠ADE=145°,
∴∠ADB=180°-145°=35°.
∵AD∥BC,
∴∠DAB=∠ADB=35°.
故答案为:35°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.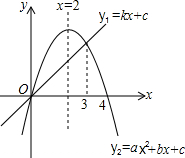 一次函数y1=kx+c与二次函数y2=ax2+bx+c的图象如图所示,则下列结论中:①k<0;②a>0;③c=0;④方程ax2+bc+c=0的两个根为0或4;⑤当y1≥y2时,x的取值范围是x≤0若x≥3.其中正确的个数有( )
一次函数y1=kx+c与二次函数y2=ax2+bx+c的图象如图所示,则下列结论中:①k<0;②a>0;③c=0;④方程ax2+bc+c=0的两个根为0或4;⑤当y1≥y2时,x的取值范围是x≤0若x≥3.其中正确的个数有( )
 一次函数y1=kx+c与二次函数y2=ax2+bx+c的图象如图所示,则下列结论中:①k<0;②a>0;③c=0;④方程ax2+bc+c=0的两个根为0或4;⑤当y1≥y2时,x的取值范围是x≤0若x≥3.其中正确的个数有( )
一次函数y1=kx+c与二次函数y2=ax2+bx+c的图象如图所示,则下列结论中:①k<0;②a>0;③c=0;④方程ax2+bc+c=0的两个根为0或4;⑤当y1≥y2时,x的取值范围是x≤0若x≥3.其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.下列各式为最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\frac{\sqrt{15}}{2}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\frac{\sqrt{12}}{5}$ |
13.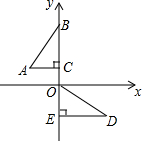 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C顺时针旋转90°,再向下平移3 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| C. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移3 |
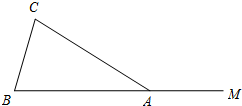 如图,在△ABC中,AB=AC,点M在BA的延长线上.
如图,在△ABC中,AB=AC,点M在BA的延长线上.