题目内容
11.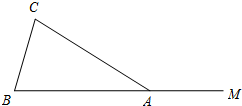 如图,在△ABC中,AB=AC,点M在BA的延长线上.
如图,在△ABC中,AB=AC,点M在BA的延长线上.(1)按下列要求作图,并在图中标明相应的字母.
①作∠CAM的平分线AN;
②作AC的中点O,连接BO,并延长BO交AN于点D,连接CD.
(2)在(1)的条件下,判断四边形ABCD的形状.并证明你的结论.
分析 (1)作一个角的平分线和线段的垂直平分线可完成作图;
(2)由AB=AC得∠ACB=∠ABC,由AN平分∠MAC得到∠MAN=∠CAN,则利用三角形外角的性质可得到∠ACB=∠CAD,所以BC∥AD,于是可证明△BOC≌△DOA,得到BC=AD,然后根据平行四边形的判定方法可判断四边形ABCD是平形四边形.
解答  解:(1)作∠MAC的角平分线AN,作AC的中垂线得到AC的中点O,连接BO,并延长BO交AN于点D,连接CD,如图;
解:(1)作∠MAC的角平分线AN,作AC的中垂线得到AC的中点O,连接BO,并延长BO交AN于点D,连接CD,如图;
(2)四边形ABCD是平形四边形,理由如下:
∵AB=AC
∴∠ACB=∠ABC,
∵AN平分∠MAC,
∴∠MAN=∠CAN,
∵∠MAC=∠ABC+∠ACB,
∴∠ACB=∠CAD,
∴BC∥AD,
∵AC的中点是O
∴AO=CO,
在△BOC和△DOA中
$\left\{\begin{array}{l}{∠OCB=∠OAD}\\{OC=OA}\\{∠BOC=∠AOD}\end{array}\right.$
∴△BOC≌△DOA,
∴BC=AD,
而BC∥AD,
∴四边形ABCD是平形四边形.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了全等三角形的判定与性质和平行四边形的判定.

练习册系列答案
相关题目
6.在函数y=$\frac{{\sqrt{x+3}}}{x-1}$中,自变量x的取值范围是( )
| A. | x≥-3且x≠1 | B. | x>-3且x≠1 | C. | x≥3 | D. | x>3 |
20.已知∠1=40°,则∠1的余角的度数是( )
| A. | 40° | B. | 50° | C. | 140° | D. | 150° |
1. 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )
 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB为( )| A. | 70° | B. | 20° | C. | 140° | D. | 35° |

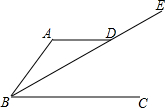 如图,AD∥BC,点E在BD的延长线上.若∠ADE=145°,则∠DBC=35°.
如图,AD∥BC,点E在BD的延长线上.若∠ADE=145°,则∠DBC=35°.