已知$\sqrt{3a+1}+\sqrt{b+1}$=0.则-a2-b2015=$\frac{8}{9}$．题目和参考答案——青夏教育精英家教网—

题目内容

15．已知$\sqrt{3a+1}+\sqrt{b+1}$=0，则-a²-b²⁰¹⁵=$\frac{8}{9}$．

分析根据非负数的性质列式求出a、b的值，然后代入代数式进行计算即可得解．

解答解：由题意得，3a+1=0，b+1=0，
解得a=-$\frac{1}{3}$，b=-1，
所以，-a²-b²⁰¹⁵=-（-$\frac{1}{3}$）²-（-1）²⁰¹⁵=-$\frac{1}{9}$+1=$\frac{8}{9}$．
故答案为：$\frac{8}{9}$．

点评本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．

练习册系列答案

6．在函数y=$\frac{{\sqrt{x+3}}}{x-1}$中，自变量x的取值范围是（　　）

3．

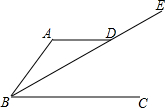如图，AD∥BC，点E在BD的延长线上．若∠ADE=145°，则∠DBC=35°．

10．

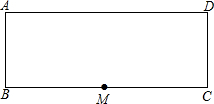如图是矩形纸片ABCD．AB=16cm，BC=40cm，M是边BC的中点，沿过M的直线翻折．若点B恰好落在边AD上，那么折痕长度为10$\sqrt{5}$或8$\sqrt{5}$cm．

20．已知∠1=40°，则∠1的余角的度数是（　　）

（a³）²=a⁵

4．不等式组$\left\{\begin{array}{l}{3x≥9}\\{x＜5}\end{array}\right.$的整数解共有（　　）

5．

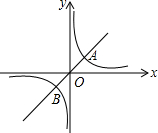如图，反比例函数y=$\frac{k}{x}$（k＞0）与正比例函数y=ax相交于A（1，k），B（-k，-1）两点．
（1）求反比例函数和正比例函数的解析式；
（2）将正比例函数y=ax的图象平移，得到一次函数y=ax+b的图象，与函数y=$\frac{k}{x}$（k＞0）的图象交于C（x₁，y₁），D（x₂，y₂），且|x₁-x₂|•|y₁-y₂|=5，求b的值．

试题分类