题目内容
已知正比例函数y=k1x(k1≠0)与反比例函数y=
(k2≠0)的图象有一个交点的坐标为(-2,-1),则它们的另一个交点的坐标是( )
| k2 |
| x |
| A、( 2,-1) |
| B、(-2,-1) |
| C、(-2,1) |
| D、(2,1) |
考点:反比例函数图象的对称性
专题:数形结合
分析:根据反比例函数图象的对称性得到反比例函数图象与正比例函数图象的两个交点关于原点对称,所以写出点(-2,-1)关于原点对称的点的坐标即可.
解答:解:∵正比例函数y=k1x(k1≠0)与反比例函数y=
(k2≠0)的图象的两个交点关于原点对称,
而一个交点的坐标为(-2,-1),
∴它们的另一个交点的坐标是(2,1).
故选D.
| k2 |
| x |
而一个交点的坐标为(-2,-1),
∴它们的另一个交点的坐标是(2,1).
故选D.
点评:本题主要考查了反比例函数图象的中心对称性,要求同学们要熟练掌握.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
有一装有6个红球,3个白球,2个黄球(所有球除颜色外均相同)的袋子中任意摸出一个球,则摸到的可能性最大的球的是( )
| A、红球 | B、白球 | C、黄球 | D、一样大 |
如图是一个简单的数值运算程序,当输入的x值为-2时,输出的值为( )


| A、26 | B、20 | C、16 | D、22 |
把△ABC三边的长度都扩大为原来的3倍,则锐角A的余弦函数值( )
| A、不变 | ||
B、缩小为原来的
| ||
| C、扩大为原来的3倍 | ||
| D、不能确定 |
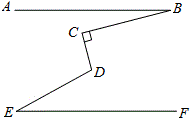 如图,AB∥EF,∠C=90°,试探究:∠B,∠CDE,∠E之间的数量关系,并说明理由.
如图,AB∥EF,∠C=90°,试探究:∠B,∠CDE,∠E之间的数量关系,并说明理由. 如图,A为反比例函数y=
如图,A为反比例函数y= 反比例函数y=
反比例函数y=