题目内容
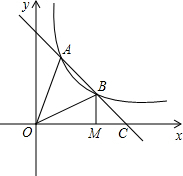 如图,直线AB交双曲线y=
如图,直线AB交双曲线y=| k |
| x |
| 1 |
| 2 |
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:设B坐标为(a,b),将B坐标代入反比例解析式求出得到ab=k,确定出OM与BM的长,根据OM=3MC,表示出MC长,进而表示出三角形BOM与三角形BMC的面积,两面积之和表示出三角形BOC面积,由BC为AB的一半,不妨设点O到AC的距离为h,求出三角形BOC与三角形AOB面积之比,确定出三角形AOC面积,利用反比例函数k的几何意义即可求出k的值.
解答:解:设B(a,b),
∵点B在函数y=
上,
∴ab=k,且OM=a,BM=b,
∵OM=3MC,
∴MC=
a,
∴S△BOM=
ab=
k,S△BMC=
×
ab=
ab=
k,
∴S△BOC=S△BOM+S△BMC=
k+
k=
k,
∵BC=
AB,不妨设点O到AC的距离为h,
则
=
=
=
,
∴S△AOB=2S△BOC=
k,
∴S△AOC=S△AOB+S△BOC=
k+
k=2k,
∵S△AOC=8.
∴2k=8,
∴k=4.
∵点B在函数y=
| k |
| x |
∴ab=k,且OM=a,BM=b,
∵OM=3MC,
∴MC=
| 1 |
| 3 |
∴S△BOM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
∴S△BOC=S△BOM+S△BMC=
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
∵BC=
| 1 |
| 2 |
则
| S△BOC |
| S△AOB |
| ||
|
| BC |
| AB |
| 1 |
| 2 |
∴S△AOB=2S△BOC=
| 4 |
| 3 |
∴S△AOC=S△AOB+S△BOC=
| 4 |
| 3 |
| 2 |
| 3 |
∵S△AOC=8.
∴2k=8,
∴k=4.
点评:此题考查了反比例函数与一次函数的交点问题,熟练掌握反比例函数的性质是解本题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
一个代数式减去x2-y2等于x2+2y2,则这个代数式是( )
| A、-3y2 |
| B、2x2+y2 |
| C、3y2-2x2 |
| D、3y2 |
等腰三角形的两内角度数之比是1:2,则顶角的度数是( )
| A、90° | B、45° |
| C、36° | D、90°或36° |
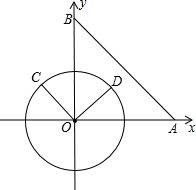 在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中C、O、D按逆时针方向排列),连接AB.
在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中C、O、D按逆时针方向排列),连接AB. 如图,一块长方形菜地属于小王、小李、小赵和小孙家,已知前三家菜地面积依次为0.8亩、0.4亩、1.2亩,你能根据所提供的信息求出小孙家的菜地面积吗?
如图,一块长方形菜地属于小王、小李、小赵和小孙家,已知前三家菜地面积依次为0.8亩、0.4亩、1.2亩,你能根据所提供的信息求出小孙家的菜地面积吗? 如图,直线AB、CD被直线EF所截,如果同位角∠1=∠3,那么内错角∠2与∠3相等吗?同旁内角∠3与∠5互补吗?请说明理由.
如图,直线AB、CD被直线EF所截,如果同位角∠1=∠3,那么内错角∠2与∠3相等吗?同旁内角∠3与∠5互补吗?请说明理由. 如图,四个村庄A、B、C、D分别在正方形ABCD的四个顶点处,E是通往A,B村庄公路上的一所小学,且BE=2km,AE=3BE,打算在A,C村庄的公路上修一个自来水站P向B,E两地供水.请问P修在A,C村庄的公路上的什么位置,才能使PB+PE的值最小?并求出最小值.
如图,四个村庄A、B、C、D分别在正方形ABCD的四个顶点处,E是通往A,B村庄公路上的一所小学,且BE=2km,AE=3BE,打算在A,C村庄的公路上修一个自来水站P向B,E两地供水.请问P修在A,C村庄的公路上的什么位置,才能使PB+PE的值最小?并求出最小值. 几何问题:
几何问题: