题目内容
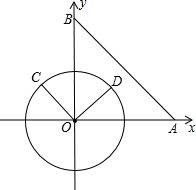 在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中C、O、D按逆时针方向排列),连接AB.
在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中C、O、D按逆时针方向排列),连接AB.(1)当OC∥AB时,∠BOC的度数为
(2)连接AD,当OC∥AD时,
①求出点C的坐标;
②直线BC是否为⊙O的切线?请作出判断,并说明理由.
(3)连接AC,BC,点C在⊙O上的运动过程中,当△ABC的面积最大时,请直接写出△ABC的最大面积.
考点:圆的综合题
专题:
分析:(1)根据点A和点B坐标易得△OAB为等腰直角三角形,则∠OBA=45°,由于OC∥AB,所以当C点在y轴左侧时,有∠BOC=∠OBA=45°;当C点在y轴右侧时,有∠BOC=180°-∠OBA=135°,从而得出答案;
(2)①过C点作CF⊥x轴于F,易证Rt△OCF∽Rt△AOD,则
=
,即
=
,得出CF=
,再利用勾股定理计算出OF=
=
,则可得到C点坐标;
②由于OC=3,OF=
,得出∠COF=30°,则可得到BOC=60°,∠AOD=60°,然后根据“SAS”判断△BOC≌△AOD,从而得出∠BCO=∠ADO=90°,再根据切线的判定定理可确定直线BC为⊙O的切线.
(3)由△OAB为等腰直角三角形得AB=
OA=6
,根据三角形面积公式得到当点C到AB的距离最大时,△ABC的面积最大,过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,此时C点到AB的距离的最大值为CE的长然后利用等腰直角三角形的性质计算出OE,然后计算△ABC的面积;
(2)①过C点作CF⊥x轴于F,易证Rt△OCF∽Rt△AOD,则
| CF |
| OD |
| OC |
| OA |
| CF |
| 3 |
| 3 |
| 6 |
| 3 |
| 2 |
| OC2-CF2 |
3
| ||
| 2 |
②由于OC=3,OF=
| 3 |
| 2 |
(3)由△OAB为等腰直角三角形得AB=
| 2 |
| 2 |
解答:解:(1)∵点A(6,0),点B(0,6),
∴OA=OB=6,
∴△OAB为等腰直角三角形,
∴∠OBA=45°,
∵OC∥AB,
∴当C点在y轴左侧时,∠BOC=∠OBA=45°,
当C点在y轴右侧时,∠BOC=180°-∠OBA=135°,
∴∠OBA=45°或135°;
故答案为:45°或135°.
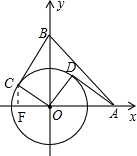 (2)如图:当C在第二象限时,过点C作CF⊥x轴于F,则∠CFO=90°,
(2)如图:当C在第二象限时,过点C作CF⊥x轴于F,则∠CFO=90°,
∵OC∥AD,
∴∠COF=∠DAO,
∴∠ADO=∠COD=90°,
∴∠ADO=∠CFO,
∴△OCF∽△AOD,
∴
=
,即
=
,
解得:CF=
,在Rt△OCF中,OF=
=
,
∴C点的坐标为(-
,
),
同理,当C在第一象限时,C点的坐标是(
,
),
∴C点的坐标为(-
,
),(
,
);
②直线BC为为⊙O的切线,理由如下:
如图:在Rt△OCF中,OC=3,CF=
,
∴sin∠COF=
=
,
∴∠COF=30°,
∴∠OAD=30°,
∴∠BOC=60°,∠AOD=60°,
在△BOC和△AOD中,
,
∴△BOC≌△AOD(SAS),
∴∠BCO=∠ADO=90°,
∴OC⊥BC,
∴直线BC是⊙O的切线;
(3)∵△OAB为等腰直角三角形,
∴AB=
OA=6
,
 ∴当点C到AB的距离最大时,△ABC的面积最大,
∴当点C到AB的距离最大时,△ABC的面积最大,
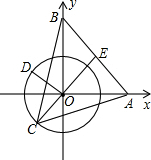
过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,
如图:此时C点到AB的距离最大值为CE的长,
∵△OAB为等腰直角三角形,
∴OE=
AB=3
,
∴CE=OC+OE=3+3
,△ABC的面积=
CE•AB=
×(3+3
)×6
=9
+18,
当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时,△ABC的面积最大,最大值为9
+18.
∴OA=OB=6,
∴△OAB为等腰直角三角形,
∴∠OBA=45°,
∵OC∥AB,
∴当C点在y轴左侧时,∠BOC=∠OBA=45°,
当C点在y轴右侧时,∠BOC=180°-∠OBA=135°,
∴∠OBA=45°或135°;
故答案为:45°或135°.
 (2)如图:当C在第二象限时,过点C作CF⊥x轴于F,则∠CFO=90°,
(2)如图:当C在第二象限时,过点C作CF⊥x轴于F,则∠CFO=90°,∵OC∥AD,
∴∠COF=∠DAO,
∴∠ADO=∠COD=90°,
∴∠ADO=∠CFO,
∴△OCF∽△AOD,
∴
| CF |
| OD |
| OC |
| OA |
| CF |
| 3 |
| 3 |
| 6 |
解得:CF=
| 3 |
| 2 |
| OC2-CF2 |
3
| ||
| 2 |
∴C点的坐标为(-
3
| ||
| 2 |
| 3 |
| 2 |
同理,当C在第一象限时,C点的坐标是(
3
| ||
| 2 |
| 3 |
| 2 |
∴C点的坐标为(-
3
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
②直线BC为为⊙O的切线,理由如下:
如图:在Rt△OCF中,OC=3,CF=
| 3 |
| 2 |
∴sin∠COF=
| CF |
| OC |
| 1 |
| 2 |
∴∠COF=30°,
∴∠OAD=30°,
∴∠BOC=60°,∠AOD=60°,
在△BOC和△AOD中,
|
∴△BOC≌△AOD(SAS),
∴∠BCO=∠ADO=90°,
∴OC⊥BC,
∴直线BC是⊙O的切线;
(3)∵△OAB为等腰直角三角形,
∴AB=
| 2 |
| 2 |
 ∴当点C到AB的距离最大时,△ABC的面积最大,
∴当点C到AB的距离最大时,△ABC的面积最大,过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,
如图:此时C点到AB的距离最大值为CE的长,
∵△OAB为等腰直角三角形,
∴OE=
| 1 |
| 2 |
| 2 |
∴CE=OC+OE=3+3
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时,△ABC的面积最大,最大值为9
| 2 |
点评:本题考查了圆的综合题,用到的知识点是切线的判定定理、平行线的性质和等腰直角三角形的判定与性质;熟练运用勾股定理和相似比进行几何计算是本题的关键.

练习册系列答案
相关题目
|-
|的相反数是( )
| 1 |
| 2014 |
| A、2014 | ||
| B、-2014 | ||
C、
| ||
D、-
|
把多项式a3-4a分解因式,下列结果正确的是( )
| A、a3-4a |
| B、(a-2)(a+2) |
| C、a(a+2)(a-2) |
| D、(a-2)2-4 |




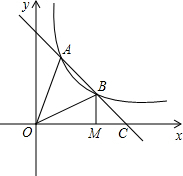 如图,直线AB交双曲线
如图,直线AB交双曲线