题目内容
在平面直角坐标系中,点A、B、C的坐标分别为(2,0),(3,
),(1,
),点D、E的坐标分别为(m,
m),(n,
n)(m、n为非负数),则CE+DE+DB的最小值是 .
| 3 |
| 3 |
| 3 |
| ||
| 3 |
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:根据点D、E的坐标分别为(m,
m),(n,
n)(m、n为非负数),可知直线OD,直线OE的解析式,分别找到点C关于直线OE的对称点C′,点B关于直线OF的对称点B′,连接C′B′,交OD于D,交OE于E,此时CE+DE+BD的值最小,求出CE+DE+BD=C′B′,根据两点间的距离公式求出即可.
| 3 |
| ||
| 3 |
解答: 解:如图所示:
解:如图所示:
∵点D、E的坐标分别为(m,
m),(n,
n)(m、n为非负数),
∴直线OD的解析式为y=
x,直线OE的解析式y=
x,
设点C关于直线OE的对称点C′所在直线CC′的解析式为y=-
x+b,
把C的坐标(1,
)代入可得-
+b=
,解得b=2
,
故直线CC′的解析式为y=-
x+2
,
联立直线OE的解析式和直线CC′的解析式可得
,
解得
.
故交点坐标为(1.5,
),
∴点C′坐标为(2,0),
设点B关于直线OD的对称点B′所在直线BB′的解析式为y=-
x+b′,
把B的坐标(3,
)代入可得-
+b′=
,解得b′=2
,
故直线BB′的解析式为y=-
x+2
,
联立直线OD的解析式和直线BB′的解析式可得
,
解得
,
故交点坐标为(1.5,
),
∴点B′坐标为(0,2
),
则B′C′=
=4,即CE+DE+DB的最小值是4.
故答案为:4.
 解:如图所示:
解:如图所示:∵点D、E的坐标分别为(m,
| 3 |
| ||
| 3 |
∴直线OD的解析式为y=
| 3 |
| ||
| 3 |
设点C关于直线OE的对称点C′所在直线CC′的解析式为y=-
| 3 |
把C的坐标(1,
| 3 |
| 3 |
| 3 |
| 3 |
故直线CC′的解析式为y=-
| 3 |
| 3 |
联立直线OE的解析式和直线CC′的解析式可得
|
解得
|
故交点坐标为(1.5,
| ||
| 2 |
∴点C′坐标为(2,0),
设点B关于直线OD的对称点B′所在直线BB′的解析式为y=-
| ||
| 3 |
把B的坐标(3,
| 3 |
| 3 |
| 3 |
| 3 |
故直线BB′的解析式为y=-
| ||
| 3 |
| 3 |
联立直线OD的解析式和直线BB′的解析式可得
|
解得
|
故交点坐标为(1.5,
3
| ||
| 2 |
∴点B′坐标为(0,2
| 3 |
则B′C′=
22+(2
|
故答案为:4.
点评:本题考查了轴对称-最短路线,两点间的距离公式的应用,关键是找出符合条件的点D和E的位置.

练习册系列答案
相关题目
|-
|的相反数是( )
| 1 |
| 2014 |
| A、2014 | ||
| B、-2014 | ||
C、
| ||
D、-
|
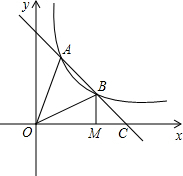 如图,直线AB交双曲线
如图,直线AB交双曲线