题目内容
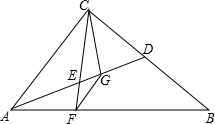如图，△ABC中，∠ACB=90°，AD为BC边上的中线，点E为AD中点，CE的延长线交AB于点F，FG∥AC，交AD于点G，连接CG．求证：（1）四边形ACGF是等腰梯形；
（2）BF=2CG．
考点：等腰梯形的判定
专题：证明题
分析：（1）根据已知条件得出AE=CE，再根据FG∥AC，得出EF=GE，在△AEF和△CEG中，根据SAS得出△AEF≌△CEG，从而得出CG=AF，即可证出四边形ACGF是等腰梯形；
（2）过D作DM平行AC交AB于M，过E作EN平行AC交AB于N，根据E为AD中点，EN∥AC∥DM，得出
=
=
=
，再根据D为BC中点，DM∥AC，得出
=
=
=
，从而得出FB=2AF，再根据AF=CG，即可得出BF=2CG．
（2）过D作DM平行AC交AB于M，过E作EN平行AC交AB于N，根据E为AD中点，EN∥AC∥DM，得出
| EN |
| DM |
| AN |
| AM |
| AE |
| AD |
| 1 |
| 2 |
| DM |
| AC |
| BM |
| AB |
| BD |
| BC |
| 1 |
| 2 |
解答：解：（1）∵∠ACB=90°，E为AD中点，
∴AE=CE，
∵FG∥AC，
∴
=
，
∴EF=GE，
在△AEF和△CEG中，
，
∴△AEF≌△CEG（SAS），
∴CG=AF，
∴四边形ACGF是等腰梯形；
（2）过D作DM平行AC交AB于M，过E作EN平行AC交AB于N，
∵E为AD中点，
EN∥AC∥DM，
∴
=
=
=
，
∵D为BC中点，DM∥AC，
∴
=
=
=
∴
=
•
=
，
∴
=
=
，
∴
=
，
∴
=
=
，
∴
=
=
∴
=
=
，
=
=
，
=AF（AB-AF）=
=
，
∴FB=2AF，
又∵AF=CG，
∴BF=2CG．
∴AE=CE，
∵FG∥AC，
∴
| EF |
| CE |
| GE |
| AE |
∴EF=GE，
在△AEF和△CEG中，
|
∴△AEF≌△CEG（SAS），
∴CG=AF，
∴四边形ACGF是等腰梯形；
（2）过D作DM平行AC交AB于M，过E作EN平行AC交AB于N，
∵E为AD中点，
EN∥AC∥DM，∴
| EN |
| DM |
| AN |
| AM |
| AE |
| AD |
| 1 |
| 2 |
∵D为BC中点，DM∥AC，
∴
| DM |
| AC |
| BM |
| AB |
| BD |
| BC |
| 1 |
| 2 |
∴
| EN |
| AC |
| EN |
| DM |
| DM |
| AC |
| 1 |
| 4 |
∴
| EF |
| CF |
| EN |
| AC |
| 1 |
| 4 |
∴
| EF |
| CE |
| 1 |
| 3 |
∴
| GF |
| AC |
| EF |
| CE |
| 1 |
| 3 |
∴
| GF |
| DM |
| GF | ||
|
| 2 |
| 3 |
∴
| AF |
| AM |
| GF |
| DM |
| 2 |
| 3 |
| AF |
| AB |
| AF |
| 2AM |
| 1 |
| 3 |
| AF |
| FB |
| 1 |
| 3-1 |
| 1 |
| 2 |
∴FB=2AF，
又∵AF=CG，
∴BF=2CG．
点评：此题考查了等腰梯形的判定，用到的知识点是全等三角形的判定与性质、等腰梯形的判定、平行线的性质等知识点，关键是根据题意做出辅助线，构造相应的三角形．
练习册系列答案
相关题目
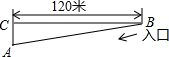煤矿井下A点的海拔高度为-174.8米，已知从A到B的水平距离为120米，每经过水平距离10米，海拔上升（或下降）0.4米．
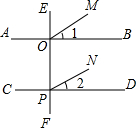如图，EF⊥AB，垂足为O，EF⊥CD，垂足为P，且∠1=∠2，说出OM与PN的位置关系，并说明理由．
有两棵树，一棵高10米，另一颗高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行多什么米？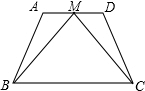
已知梯形ABCD中，AD∥BC，M是AD的中点，∠MBC=∠MCB，求证：梯形ABCD是等腰梯形．
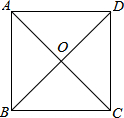如图，四边形ABCD中，AB=BC=CD=DA，对角线AC与BD相交于点O，要使ABCD是正方形，则需增加一个条件是
如图，两同心圆间的圆环的面积为16π，过小圆上任意一点P作大圆的弦AB，则PA•PB的值是（ ）| A、16 | B、16π | C、4 | D、4π |
有理数a，b在数轴上（如图），那么