题目内容
 如图,两同心圆间的圆环的面积为16π,过小圆上任意一点P作大圆的弦AB,则PA•PB的值是( )
如图,两同心圆间的圆环的面积为16π,过小圆上任意一点P作大圆的弦AB,则PA•PB的值是( )| A、16 | B、16π | C、4 | D、4π |
考点:切割线定理
专题:
分析:过P点作大圆的直径CD,如图,设大圆半径为R,小圆半径为r,根据相交弦定理得到PA•PB=(OC-OP)•(OP+OD)=R2-r2,再利用πR2-πr2=16π得到R2-r2=16,所以PA•PB=16.
解答:解:过P点作大圆的直径CD,如图,设大圆半径为R,小圆半径为r,
∵PA•PB=PC•PD,
∴PA•PB=(OC-OP)•(OP+OD)
=(R-r)(R+r)
=R2-r2,
∵两同心圆间的圆环(即图中阴影部分)的面积为16π,
∴πR2-πr2=16π,
∴R2-r2=16,
∴PA•PB=16.
故选A.

∵PA•PB=PC•PD,
∴PA•PB=(OC-OP)•(OP+OD)
=(R-r)(R+r)
=R2-r2,
∵两同心圆间的圆环(即图中阴影部分)的面积为16π,
∴πR2-πr2=16π,
∴R2-r2=16,
∴PA•PB=16.
故选A.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了相交弦定理.

练习册系列答案
相关题目
2008年6月1日起全国商品零售场所开始实行“塑料购物袋有偿使用制度”,截止到2012年5月底全国大约节约塑料袋8.984亿个,用科学记数法表示约为(保留两个有效数字)( )
| A、8.984×108 |
| B、8.98×108 |
| C、9×108 |
| D、9.0×108 |
在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )
A、 |
B、 |
C、 |
D、 |
二次函数y=-
x2+
x+1000的图象经过第一象限的整格点(即纵、横坐标是正整数的点) 共有( )个.
| 1 |
| 2 |
| 1999 |
| 2 |
| A、1 000 |
| B、1 001 |
| C、1 999 |
| D、2 001 |
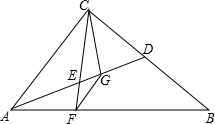 如图,△ABC中,∠ACB=90°,AD为BC边上的中线,点E为AD中点,CE的延长线交AB于点F,FG∥AC,交AD于点G,连接CG.求证:
如图,△ABC中,∠ACB=90°,AD为BC边上的中线,点E为AD中点,CE的延长线交AB于点F,FG∥AC,交AD于点G,连接CG.求证: 如图,直线AB,CD,EF相交于点O,EF⊥AB,OG平分∠COF,若∠COG:∠BOC=1:7,求∠DOF的大小.
如图,直线AB,CD,EF相交于点O,EF⊥AB,OG平分∠COF,若∠COG:∠BOC=1:7,求∠DOF的大小.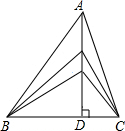 如图,△ABC边BC的长为10cm,BC边上的高为AD,当点A沿AD所在直线向点D运动时,三角形的面积发生了变化.
如图,△ABC边BC的长为10cm,BC边上的高为AD,当点A沿AD所在直线向点D运动时,三角形的面积发生了变化. 正比例函数y=kx和y=2kx(k是常数且k>0)的图象如图,它们与反比例函数y=
正比例函数y=kx和y=2kx(k是常数且k>0)的图象如图,它们与反比例函数y=