题目内容
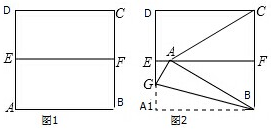 如何在一张正方形纸中折出一个等边三角形呢?如图①,对折正方形纸片ABCD,得到折痕EF,沿过点B的折痕将A角翻折,如图②使得点A落在EF上,连接AC,则△ABC即为等边三角形,请你说明这样做的道理.
如何在一张正方形纸中折出一个等边三角形呢?如图①,对折正方形纸片ABCD,得到折痕EF,沿过点B的折痕将A角翻折,如图②使得点A落在EF上,连接AC,则△ABC即为等边三角形,请你说明这样做的道理.考点:翻折变换(折叠问题)
专题:
分析:首先判断出A1B=AB=BC,结合BF=
BC,求出∠ABF=60°问题即可解决.
| 1 |
| 2 |
解答: 解:如图2,
解:如图2,
由题意得:A1B=AB,BF=
BC;
∵四边形A1BCD为正方形,
∴A1B=BC,
∴BF=
AB;
∵△ABF为直角三角形,
∴∠ABF=60°;
由题意得:AF⊥BC,BF=CF,
∴AB=AC,
∴△ABC为等边三角形.
 解:如图2,
解:如图2,由题意得:A1B=AB,BF=
| 1 |
| 2 |
∵四边形A1BCD为正方形,
∴A1B=BC,
∴BF=
| 1 |
| 2 |
∵△ABF为直角三角形,
∴∠ABF=60°;
由题意得:AF⊥BC,BF=CF,
∴AB=AC,
∴△ABC为等边三角形.
点评:该命题考查了翻折变换及其应用问题;灵活运用翻折变换、全等三角形的性质等几何知识判断出图中相等的边或角是解题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
若关于x的一元二次方程ax2+bx+5=0(a≠0)的解是x=1,则2010-a-b的值是( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |
若函数y=axa2-2a-6是二次函数且图象开口向上,则a=( )
| A、-2 | B、4 |
| C、4或-2 | D、4或3 |
 如图,某学校要在校园内墙边的空地上修建一个长方形的存车处,存车处的一面靠墙(墙长22m),另外三面用90m长的铁栅栏围起来,如果这个存车处的面积为700m2,求这个长方形存车处的长和宽.
如图,某学校要在校园内墙边的空地上修建一个长方形的存车处,存车处的一面靠墙(墙长22m),另外三面用90m长的铁栅栏围起来,如果这个存车处的面积为700m2,求这个长方形存车处的长和宽.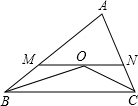 如图,O是△ABC中∠ABC平分线上的一点,过O作BC的平行线与AB、AC分别交于M、N两点,且有MN=BM+CN,连结CO.求证:CO平分∠ACB.
如图,O是△ABC中∠ABC平分线上的一点,过O作BC的平行线与AB、AC分别交于M、N两点,且有MN=BM+CN,连结CO.求证:CO平分∠ACB.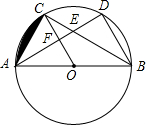 如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为弧AD的中点;
如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为弧AD的中点;