题目内容
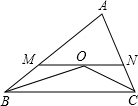 如图,O是△ABC中∠ABC平分线上的一点,过O作BC的平行线与AB、AC分别交于M、N两点,且有MN=BM+CN,连结CO.求证:CO平分∠ACB.
如图,O是△ABC中∠ABC平分线上的一点,过O作BC的平行线与AB、AC分别交于M、N两点,且有MN=BM+CN,连结CO.求证:CO平分∠ACB.考点:等腰三角形的判定与性质,平行线的性质
专题:证明题
分析:由BO平分∠ABC,MN∥BC,可得∠1=∠3,∠4=∠5,由∠1=∠3可得BM=OM,由MN=BM+CN,MN=MO+NO,可得CN=ON,所以∠4=∠6,进而得到∠5=∠6.所以CO平分∠ACB.
解答:证明:如图,
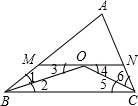
∵BO平分∠ABC,
∴∠1=∠2,
∵MN∥BC,
∴∠2=∠3,∠4=∠5,
∴∠1=∠3,
∴BM=MO,
∵MN=BM+CN,MN=MO+NO,
∴ON=NC,
∴∠4=∠6,
∴∠5=∠6,
∴CO平分∠ACB.

∵BO平分∠ABC,
∴∠1=∠2,
∵MN∥BC,
∴∠2=∠3,∠4=∠5,
∴∠1=∠3,
∴BM=MO,
∵MN=BM+CN,MN=MO+NO,
∴ON=NC,
∴∠4=∠6,
∴∠5=∠6,
∴CO平分∠ACB.
点评:此题考查了等腰三角形的判定,平行线的性质,利用了等量代换的思想,熟练掌握性质与判定是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
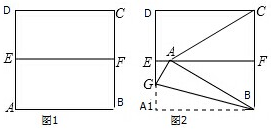 如何在一张正方形纸中折出一个等边三角形呢?如图①,对折正方形纸片ABCD,得到折痕EF,沿过点B的折痕将A角翻折,如图②使得点A落在EF上,连接AC,则△ABC即为等边三角形,请你说明这样做的道理.
如何在一张正方形纸中折出一个等边三角形呢?如图①,对折正方形纸片ABCD,得到折痕EF,沿过点B的折痕将A角翻折,如图②使得点A落在EF上,连接AC,则△ABC即为等边三角形,请你说明这样做的道理.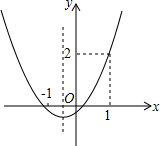 已知抛物线y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②a+b+c=2;③2a-b>0;④b>1.其中正确的结论个数是( )
已知抛物线y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②a+b+c=2;③2a-b>0;④b>1.其中正确的结论个数是( )