题目内容
18. 如图,直角坐标系中的网格由单位正方形构成.△ABC中,A点坐标为(2,3)、B(-2,0)、C(0,-1).
如图,直角坐标系中的网格由单位正方形构成.△ABC中,A点坐标为(2,3)、B(-2,0)、C(0,-1).(1)AB的长为5,∠ACB的度数为90°;
(2)若以A、B、C及点D为顶点的四边形为平行四边形,请写出D点的坐标(0,4),并在图中画出其中一个平行四边形.
分析 (1)由勾股定理即可求得AB,BC,AC的值,然后由勾股定理逆定理,可判定△ABC是直角三角形;
(2)首先根据题意画出图形,然后根据图可求得平行四边形中D点的坐标.
解答 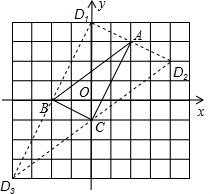 解:(1)根据题意得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5;
解:(1)根据题意得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5;
∴AB2=25,BC2=12+22=5,AC2=22+42=20,
∴BC2+AC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°;
(2)如图,D1(0,4)或D2(4,2)或D3(-4,4)(填一个即可).
故答案为:(1)5,90°;(2)答案不唯一:如(0,4)或(4,2)或(-4,-4)(填一个即可).
点评 此题考查了平行四边形的性质以及勾股定理与逆定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下列变形是因式分解的是( )
| A. | x2+6x+8=x(x+6)+8 | B. | (x+2)(x-2)=x2-4 | C. | ${x^2}+3x={x^2}(1+\frac{3}{x})$ | D. | x2-3x+2=(x-1)(x-2) |
9.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{16}$ | B. | $\sqrt{1.2}$ | C. | $\sqrt{15}$ | D. | $\sqrt{\frac{1}{3}}$ |
6.在函数y=$\frac{\sqrt{2-x}}{x+1}$中,自变量x的取值范围是( )
| A. | x≥2且x≠-1 | B. | x≤2且x≠-1 | C. | x≥2 | D. | x≤2 |
13. 如图,直线y=kx+b经过点A(0,3),B(1,2),则关于x的不等式0≤kx+b<2x的解集为( )
如图,直线y=kx+b经过点A(0,3),B(1,2),则关于x的不等式0≤kx+b<2x的解集为( )
 如图,直线y=kx+b经过点A(0,3),B(1,2),则关于x的不等式0≤kx+b<2x的解集为( )
如图,直线y=kx+b经过点A(0,3),B(1,2),则关于x的不等式0≤kx+b<2x的解集为( )| A. | 1<x≤3 | B. | 1≤x<3 | C. | x>1 | D. | 无法确定 |
3.如果关于x的不等式 (a+2016)x>a+2016的解集为x<1,那么a的取值范围是( )
| A. | a>-2016 | B. | a<-2016 | C. | a>2016 | D. | a<2016 |
8.下列各式中,不能运用平方差公式计算的是( )
| A. | (ab-1)(ab+1) | B. | (2x-1)(-1+2x) | C. | (-2x-y)(2x-y) | D. | (-a+5)(-a-5) |
 如图,一张矩形纸片ABCD中,AD>AB将矩形纸片ABCD沿过点A的直线折叠,使点D落到BC边上的点D′,折痕AE交DC于点E.
如图,一张矩形纸片ABCD中,AD>AB将矩形纸片ABCD沿过点A的直线折叠,使点D落到BC边上的点D′,折痕AE交DC于点E.