题目内容
 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,过C作CD⊥PA,垂足为D,∠DAC=∠CAE.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,过C作CD⊥PA,垂足为D,∠DAC=∠CAE.(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若CD=4,AD=2,试求
| AB |
| AE |
考点:切线的判定
专题:
分析:(1)连接OC,根据OA=OC推出∠OCA=∠OAC,因为∠DAC=∠CAE.可得∠DAC=∠OCA,推出OC∥AD,得出OC⊥CD,根据切线的判定推出即可;
(2)过O作OM⊥AB于M.利用已知和切线的性质可得四边形DMOC是矩形,从而得到OC=DM,OM=CD=4.设半径为x,在Rt△AMO中利用勾股定理列方程,从而求得半径,继而得到AE的长,再利用勾股定理求得AM的长度,再利用垂径定理求得AB的长度,从而得到答案.
(2)过O作OM⊥AB于M.利用已知和切线的性质可得四边形DMOC是矩形,从而得到OC=DM,OM=CD=4.设半径为x,在Rt△AMO中利用勾股定理列方程,从而求得半径,继而得到AE的长,再利用勾股定理求得AM的长度,再利用垂径定理求得AB的长度,从而得到答案.
解答:解:(1)CD与⊙O相切,
理由: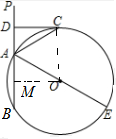
连接OC.
∵OC=OA,
∴∠OAC=∠OCA.
∵∠DAC=∠CAE,
即∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC.
∵CD⊥PA,
∴∠ADC=∠OCD=90°,
即 CD⊥OC,点C在⊙O上,
∴CD是⊙O的切线;
(2)过O作OM⊥AB于M.即∠OMA=90°,
∵∠MDC=∠OMA=∠DCO=90°,
∴四边形DMOC是矩形,
∴OC=DM,OM=CD=4.
∵AD=2
设圆的半径为x,则AM=x-AD=x-2,
∵在Rt△AMO中,∠AMO=90°,根据勾股定理得:AO2=AM2+OM2.
∴x2=(x-2)2+42,
解得,x=5,
∴⊙O的半径为5,则AE=10,
∵OA=5,OM=4,
∴AM=3,
∴AB=6,
∴
=
=
.
理由:

连接OC.
∵OC=OA,
∴∠OAC=∠OCA.
∵∠DAC=∠CAE,
即∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC.
∵CD⊥PA,
∴∠ADC=∠OCD=90°,
即 CD⊥OC,点C在⊙O上,
∴CD是⊙O的切线;
(2)过O作OM⊥AB于M.即∠OMA=90°,
∵∠MDC=∠OMA=∠DCO=90°,
∴四边形DMOC是矩形,
∴OC=DM,OM=CD=4.
∵AD=2
设圆的半径为x,则AM=x-AD=x-2,
∵在Rt△AMO中,∠AMO=90°,根据勾股定理得:AO2=AM2+OM2.
∴x2=(x-2)2+42,
解得,x=5,
∴⊙O的半径为5,则AE=10,
∵OA=5,OM=4,
∴AM=3,
∴AB=6,
∴
| AB |
| AE |
| 6 |
| 10 |
| 3 |
| 5 |
点评:本题主要考查了平行线的判定和性质、切线的判定、矩形的性质和判定,勾股定理、垂径定理等知识点,主要考查学生综合运用定理进行推理的能力及利用方程思想求解线段长度的方法.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
若3x=4,9y=7,则3x-2y的值为( )
A、
| ||
B、
| ||
| C、-9 | ||
D、
|
在平面直角坐标系上,点(4,6)先向左平移6个单位,再将得到的点的坐标关于x轴对称,得到的点位于( )
| A、x轴上 | B、y轴上 |
| C、第三象限 | D、第四象限 |


 如图,矩形ABCD中,E为对角线BD上一点,连接AE交CD于G,交BC延长线于F,∠DAE=∠DCE,∠AEB=∠CEB.
如图,矩形ABCD中,E为对角线BD上一点,连接AE交CD于G,交BC延长线于F,∠DAE=∠DCE,∠AEB=∠CEB.