题目内容
17.计算:(1)(-2ab2)2•(3a2b-2ab-1);
(2)4(a-b)2-(2a+b)(-b+2a);
(3)(x+3y)(x2+9y2)(x-3y);
(4)(1+x-y)(x+y-1).
分析 (1)先算积的乘方,再进一步按照整式的乘法计算;
(2)(4)利用平方差公式和完全平方公式计算,再进一步合并即可;
(3)逐步利用平方差公式计算.
解答 解:(1)原式=4a2b4•(3a2b-2ab-1)
=12a4b5-8a3b5-4a2b4;
(2)原式=4a2-8ab+4b2-(4a2-b2)
=4a2-8ab+4b2-4a2+b2
=-8ab+5b2;
(3)原式=((x2+9y2)(x2-9y2)
=x4-81y4;
(4)原式=[x+(1-y)][x-(1-y)]
=x2-(1-y)2
=x2-y2+2y-1.
点评 此题考查整式的混合运算,掌握运算方法和运算顺序是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若不等式组$\left\{\begin{array}{l}{x>2a+3}\\{x<5}\end{array}\right.$无解,那么a的取值范围是( )
| A. | a>5 | B. | a≥1 | C. | a<5 | D. | a>1 |
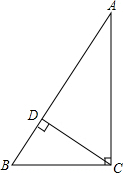 已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.