题目内容
4.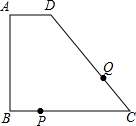 如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).
如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
(3)伴随P,Q两点的运动,线段PQ的垂直平分线为l.
①t为何值时,l经过点C?
②求当l经过点D时t的值,并求出此时刻线段PQ的长.
分析 (1)作DE⊥BC于E,根据勾股定理即可求解;
(2)线段PQ将四边形ABCD的面积分为1:2两部分,分两种情况进行求解;
(3)①当PQ的垂直平分线经过点C进行分析解答;
②当PQ的垂直平分线l经过点D时进行分析解答.
解答 解:(1)如图1,作DE⊥BC于E,
∵AD∥BC,∠A=90°,
∴四边形ABED为矩形,
∴BE=AD=1,DE=AB=3,
∴EC=BC-BE=4,
在Rt△DEC中,DE2+EC2=DC2,
∴$DC=\sqrt{{3}^{2}+{4}^{2}}=5$厘米;
(2)∵点P的速度为1厘米/秒,点Q的速度为2厘米/秒,运动时间为t秒,
∴BP=t厘米,PC=(5-t)厘米,CQ=2t厘米,QD=(5-2t)厘米,
且0<t≤2.5,
作QH⊥BC于点H,
∴DE∥QH,
∴∠DEC=∠QHC,
∵∠C=∠C,
∴△DEC∽△QHC,
∴$\frac{DE}{QH}=\frac{DC}{QC}$,
∴$\frac{3}{QH}=\frac{5}{2t}$,
∴$QH=\frac{6}{5}t$,
∴${S}_{△PQC}=\frac{1}{2}•PC•QH=\frac{1}{2}•(5-t)•\frac{6}{5}t=-\frac{3}{5}{t}^{2}$+3t,
${S}_{四边形ABCD}=\frac{1}{2}•(AD+BC)•AB=\frac{1}{2}×(1+5)×3=9$,
分两种情况讨论:
①当S△PQC:S四边形ABCD=1:3时,$-\frac{3}{5}{t}^{2}+3t=\frac{1}{3}×9$,
即t2-5t+5=0,
解得:${t}_{1}=\frac{5-\sqrt{5}}{2},{t}_{2}=\frac{5+\sqrt{5}}{2}$(舍去);
②S△PQC:S四边形ABCD=2:3时,$-\frac{3}{5}{t}^{2}+3t=\frac{2}{3}×9$,
即t2-5t+10=0,
∵△<0,
∴方程无解,
∴当t为$\frac{5-\sqrt{5}}{2}$秒时,线段PQ将四边形ABCD的面积分为1:2两部分;
(3)如图2,
①当PQ的垂直平分线l经过点C时,可知PC=QC,
∴5-t=2t,
∴3t=5,
∴t=$\frac{5}{3}$,
∴当t=$\frac{5}{3}$秒时,直线l经过点C;
②如图3,
当PQ的垂直平分线l经过点D时,
可知DQ=DP,
连接DP,则在Rt△DEP中,DP2=DE2+EP2,
∴DQ2=DE2+EP2,
∴(5-2t)2=32+(t-1)2,
∴t1=1,t2=5(舍去),
∴BP=1厘米,
∴当t=1秒时,直线l经过点D,此时点P与点E重合;
如图4,连接FQ,
∵直线l是△DPQ的对称轴,
∴△DEF≌△DQF,∠DQF=90°,EF=QF,
设EF=x厘米,则QF=x厘米,FC=(4-x)厘米,
在Rt△FQC中,FQ2+QC2=FC2,
x2+22=(4-x)2,
∴x=$\frac{3}{2}$,
∴EF=$\frac{3}{2}$厘米,
在Rt△DEF中,DE2+EF2=DF2,
∴${3}^{2}+(\frac{3}{2})^{2}=D{F}^{2}$,
∴DF=$\frac{3}{2}\sqrt{5}$厘米,
在Rt△DEF中,EG⊥DF,
∴${S}_{△DEF}=\frac{1}{2}DF•EG=\frac{1}{2}DE•EF$,
∴EG=$\frac{DE•EF}{DF}$,
∴EG=$\frac{3\sqrt{5}}{5}$厘米,
∴PQ=2EG=$\frac{6\sqrt{5}}{5}$厘米.
点评 此题考查了四边形的综合题,能够根据勾股定理、解直角三角形的知识、三角形的面积公式进行分析讨论.

| A. | (-$\frac{1}{2}$)3 | B. | -(-$\frac{1}{2}$)0 | C. | (-$\frac{1}{2}$)-2 | D. | -|$\frac{1}{2}$| |
| A. | 面积相等的两个三角形全等 | |
| B. | 矩形的四条边一定相等 | |
| C. | 一个图形和它旋转后所得图形的对应线段相等 | |
| D. | 随机投掷一枚质地均匀的硬币,落地后一定是正面朝上 |
 如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为(5,-5).
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为(5,-5).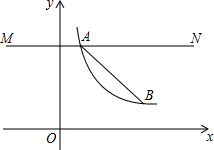 如图,点A、B是反比例函数第一象限图象上的两点,且坐标分别为(1,n),(n,$\frac{n}{4}$),直线MN过点A且与x轴平行.
如图,点A、B是反比例函数第一象限图象上的两点,且坐标分别为(1,n),(n,$\frac{n}{4}$),直线MN过点A且与x轴平行.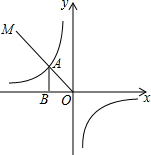 如图所示,第二象限的角平分线OM与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,已知OA=3$\sqrt{2}$,则k=-9.
如图所示,第二象限的角平分线OM与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,已知OA=3$\sqrt{2}$,则k=-9.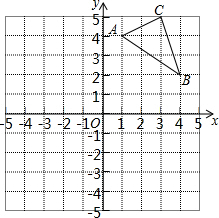 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).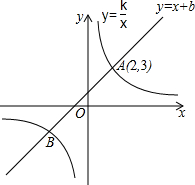 如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).
如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).