题目内容
9.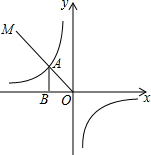 如图所示,第二象限的角平分线OM与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,已知OA=3$\sqrt{2}$,则k=-9.
如图所示,第二象限的角平分线OM与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,已知OA=3$\sqrt{2}$,则k=-9.
分析 易得点A的横纵坐标的值相等,利用勾股定理可得点A的坐标,把点A的横纵坐标代入可求得反比例函数的比例系数.
解答 解:设点A的坐标为(x,y).
∵第二象限的角平分线OM与反比例函数的图象相交于点A,
∴x=-y,
∴x2+y2=(3$\sqrt{2}$)2,
∴x=±3,
∵A在第二象限,
∴x=-3,
∴y=3,
∴A(-3,3);
设所求的函数解析式为y=函数解析式为y=$\frac{k}{x}$,A(-3,3)在反比例函数图象上,
∴k=-3×3=-9,
故答案为:-9
点评 考查了用待定系数法求反比例函数解析式;利用勾股定理求得点A的坐标是解决本题的突破点;用到的知识点为:点在反比例函数解析式上,点的横纵坐标适合函数解析式;第二象限角平分线上的点的横纵坐标相反.

练习册系列答案
相关题目
20.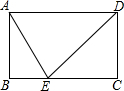 如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )
如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )
 如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )
如图,点E是矩形ABCD边BC上一点,且cos∠DAE=$\frac{1}{2}$,tan∠ADE=1,若△ABE的面积是2$\sqrt{3}$,那么△ECD的面积是( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6 | D. | 12 |
1. 如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )
如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )
 如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )
如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
 如图是由若干块小立方体搭成几何体的主视图和俯视图,则这个几何体中小立方体的个数是9或10或11或12.
如图是由若干块小立方体搭成几何体的主视图和俯视图,则这个几何体中小立方体的个数是9或10或11或12.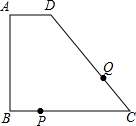 如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).
如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).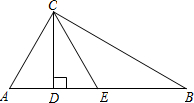 如图,已知在△ABC中,∠ACB=90°,CD为高,且CD,CE三等分∠ACB.
如图,已知在△ABC中,∠ACB=90°,CD为高,且CD,CE三等分∠ACB. 如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.
如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.