题目内容
10.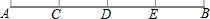 如图,点C、D、E在线段AB上,且AC=CD=DE=EB
如图,点C、D、E在线段AB上,且AC=CD=DE=EB(1)点C是线段AC的中点,点E是线段BD的中点,点D是线段AB、DE的中点;
(2)图中还有哪些相等的线段?为什么?
分析 (1)根据题意,由AC=CD=DE=EB可知:D是线段AB的中点,C是线段AD的中点,E是BC的中点;
(2)由AC=CD=DE=EB,则可得点C,D,E分别是AD,CE,DB的中点,进而可得线段相等.
解答 解:(1)∵AC=CD=DE=EB,
∴D是线段AB的中点,C是线段AD的中点,E是BC的中点,D是CE的中点,
故答案为:AC,BD,AB,DE;
(2)∵AC=CD=DE=EB,即点C,D,E分别是AD,CE,DB的中点,
∴AC+CD=CD+DE=DE+EB,即AD=CE=DB.
∴AC+CD+DE=CD+DE+EB,即AE=CB,
点评 本题考查了两点之间的距离,能够利用中点的性质求解一段线段中的相等线段是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列各式中,符合代数式书写格式是( )
| A. | 5×a | B. | 2$\frac{1}{2}$(a+b) | C. | $\frac{5(m-n)}{3}$ | D. | (a+b)h÷2 |
5. 如图中小于平角的角的个数为( )
如图中小于平角的角的个数为( )
 如图中小于平角的角的个数为( )
如图中小于平角的角的个数为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
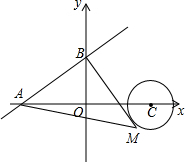 如图,已知直线y=$\frac{3}{4}$x+3与坐标轴分别交于A、B两点,M是以C(6,0)为圆心,2为半径的圆上一动点,连结MA、MB,则△MAB面积的最大值是20.
如图,已知直线y=$\frac{3}{4}$x+3与坐标轴分别交于A、B两点,M是以C(6,0)为圆心,2为半径的圆上一动点,连结MA、MB,则△MAB面积的最大值是20.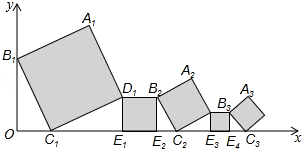 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上且坐标是(0,2),点C1、E1、E2、C2、E3、E4、C3在x轴上,C1的坐标是(1,0).B1C1∥B2C2∥B3C3,以此继续下去,则点A4到x轴的距离是$\frac{3}{8}$.
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上且坐标是(0,2),点C1、E1、E2、C2、E3、E4、C3在x轴上,C1的坐标是(1,0).B1C1∥B2C2∥B3C3,以此继续下去,则点A4到x轴的距离是$\frac{3}{8}$.