题目内容
定义一种运算:ak=ak-1+1-5([
]-[
]),其中k是正整数,且k≥2,[x]表示非负实数x的整数部分,例如[2.6]=2,[0.8]=0.若a1=1,则a2014的值为( )
| k-1 |
| 5 |
| k-2 |
| 5 |
| A、2015 | B、4 |
| C、2014 | D、5 |
考点:规律型:数字的变化类
专题:规律型
分析:根据新定义分别计算出a2=2,a3=3,a4=4,a5=5,a6=1,a7=2,a8=3,a9=4,a10=5,a11=1,由此可得a的值分别为1、2、3、4、5,且从序号1开始,每5个一循环,由于2014=5×402+4,可得a2014=a4=4.
解答:解:a1=1,
a2=a1+1-{[
]-[
]}=1+1-5(0-0)=2,
a3=a2+1-{[
]-[
]}=2+1-5(0-0)=3,
a4=a3+1-{[
]-[
]}=3+1-5(0-0)=4,
a5=a4+1-{[
]-[
]}=4+1-5(0-0)=5,
a6=a5+1-{[
]-[
]}=5+1-5(1-0)=1,
a7=a6+1-{[
]-[
]}=1+1-5(1-0)=2,
同理可得a8=3,a9=4,a10=5,a11=1,
∵2014=5×402+4,
∴a2014=a4=4.
故选B.
a2=a1+1-{[
| 2-1 |
| 5 |
| 2-2 |
| 5 |
a3=a2+1-{[
| 3-1 |
| 5 |
| 3-2 |
| 5 |
a4=a3+1-{[
| 4-1 |
| 5 |
| 4-2 |
| 5 |
a5=a4+1-{[
| 5-1 |
| 5 |
| 5-2 |
| 5 |
a6=a5+1-{[
| 6-1 |
| 5 |
| 6-2 |
| 5 |
a7=a6+1-{[
| 7-1 |
| 5 |
| 7-2 |
| 5 |
同理可得a8=3,a9=4,a10=5,a11=1,
∵2014=5×402+4,
∴a2014=a4=4.
故选B.
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
方程|x+1|+|2x-1|=1的整数解的个数为( )
| A、0 | B、1 | C、2 | D、3 |
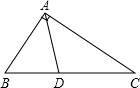 如图,△ABC中,∠BAC=90°,∠B=2∠C,D点在BC上,AD平分∠BAC,若AB=1,则BD的长为( )
如图,△ABC中,∠BAC=90°,∠B=2∠C,D点在BC上,AD平分∠BAC,若AB=1,则BD的长为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
数0是( )
| A、最小整数 | B、最小正数 |
| C、最小自然数 | D、最小有理数 |
 用若干个小立方块搭一个几何体,从正面看、从左面看如图所示,则搭这个几何体最多用
用若干个小立方块搭一个几何体,从正面看、从左面看如图所示,则搭这个几何体最多用