题目内容
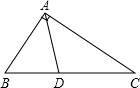如图，△ABC中，∠BAC=90°，∠B=2∠C，D点在BC上，AD平分∠BAC，若AB=1，则BD的长为（ ）A、
| ||
B、2
| ||
C、
| ||
D、2
|
考点：角平分线的性质,含30度角的直角三角形,勾股定理
专题：
分析：过C作CE∥AB，交AD的延长线于E，求出AC=CE=
，BC=2，根据相似得出比例式，代入求出即可．
| 3 |
解答：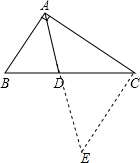
解：过C作CE∥AB，交AD的延长线于E，
则∠E=∠BAD，
∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴∠CAD=∠E，
∴AC=CE，
∵△ABC中，∠BAC=90°，∠B=2∠C，AB=1，
∴∠ACB=30°，∠B=60°，
∴BC=2AB=2，AC=
AB=
，
∴CE=
，
∵CE∥AB，
∴△ABD∽△ECD，
∴
=
，
=
，
解得：BD=
-1，
故选A．
解：过C作CE∥AB，交AD的延长线于E，则∠E=∠BAD，
∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴∠CAD=∠E，
∴AC=CE，
∵△ABC中，∠BAC=90°，∠B=2∠C，AB=1，
∴∠ACB=30°，∠B=60°，
∴BC=2AB=2，AC=
| 3 |
| 3 |
∴CE=
| 3 |
∵CE∥AB，
∴△ABD∽△ECD，
∴
| AB |
| BD |
| CE |
| CD |
| 1 |
| BD |
| ||
| 2-BD |
解得：BD=
| 3 |
故选A．
点评：本题考查了相似三角形的性质和判定，解直角三角形的应用，解此题的关键是能得出关于BD的方程，题目比较好，难度适中．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
如图，四边形ABCD与四边形CEFG都是正方形，点E在CD上，正方形ABCD的边长为2，则△BDF的面积是
如图，圆的周长为4个单位长度，在圆的4等分点处标上0，1，2，3．先让圆周上数字0所对应的数与数轴上的数-1所对应的点重合，再让数轴按逆时针方向绕在该圆上，那么数轴上的数-2007将与圆周上的数字定义一种运算：ak=ak-1+1-5([
]-[
])，其中k是正整数，且k≥2，[x]表示非负实数x的整数部分，例如[2.6]=2，[0.8]=0．若a1=1，则a2014的值为（ ）
| k-1 |
| 5 |
| k-2 |
| 5 |
| A、2015 | B、4 |
| C、2014 | D、5 |
现用边长相等且边数分别为a、b、c、d（边数不全相等）的四种正多边形刚好能进行平面镶嵌，则
+
+
+
=（ ）
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| d |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
用一个平面去截一个圆柱，截面的形状不可能是（ ）
A、 |
B、 |
C、 |
D、 |
把一次函数y=3x-1的图象向上平移3个单位，可得到的图象的函数解析式是（ ）
| A、y=3x+3 |
| B、y=3x+2 |
| C、y=3x-4 |
| D、y=3x-2 |
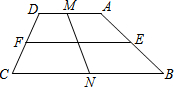如图，梯形ABCD中，AD∥BC，∠B=30°，∠C=60°，E、F、M、N分别为AB、CD、BC、DA的中点，若BC=7，MN=3，则EF为（ ）