题目内容
设a,b,c是素数,记x=b+c-a,y=c+a-b,z=a+b-c,当z2=y,
-
=2时,a,b,c能否构成三角形的三边长?证明你的结论.
| x |
| y |
考点:质数与合数
专题:
分析:首先根据题意用含有x,y,z的代数式表示出a,b,c,再根据y=z2,得到a=
,根据z为整数,a为素数求出z和a的值,进而求出b和c的值,最后判断a,b,c能否构成三角形的边长.
| z(z+1) |
| 2 |
解答:解:不能.
依题意,得 a=
(y+z),b=
(x+z),c=
(x+y).
因为y=z2,所以a=
(y+z)=
(z2+z)=
.
又由于z为整数,a为素数,
所以z=2或-3,a=3.
当z=2时,y=z2=4,x=(
+2)2=16.进而,b=9,c=10,与b,c是素数矛盾;
当z=-3时,a+b-c<0,所以a,b,c不能构成三角形的三边长.
依题意,得 a=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因为y=z2,所以a=
| 1 |
| 2 |
| 1 |
| 2 |
| z(z+1) |
| 2 |
又由于z为整数,a为素数,
所以z=2或-3,a=3.
当z=2时,y=z2=4,x=(
| y |
当z=-3时,a+b-c<0,所以a,b,c不能构成三角形的三边长.
点评:本题主要考查了质数与合数的知识,解答本题的关键根据a为素数求出z的值,进而求出a的值.

练习册系列答案
相关题目
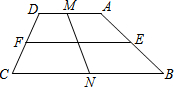 如图,梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,E、F、M、N分别为AB、CD、BC、DA的中点,若BC=7,MN=3,则EF为( )
如图,梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,E、F、M、N分别为AB、CD、BC、DA的中点,若BC=7,MN=3,则EF为( )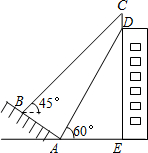 如图,某校一幢教学大楼的顶部竖有一块宣传牌CD=2米.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:
如图,某校一幢教学大楼的顶部竖有一块宣传牌CD=2米.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1: 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=